题目内容
已知m为实常数.命题p:方程
-
=1表示焦点在y轴上的椭圆;命题q:方程
+
=1表示双曲线.
(1)若命题p为真命题,求m的取值范围;
(2)若命题q为假命题,求m的取值范围;
(3)若命题p或q为真命题,且命题p且q为假命题,求m的取值范围.
| x2 |
| 2m |
| y2 |
| m-6 |
| x2 |
| m+1 |
| y2 |
| m-1 |
(1)若命题p为真命题,求m的取值范围;
(2)若命题q为假命题,求m的取值范围;
(3)若命题p或q为真命题,且命题p且q为假命题,求m的取值范围.
分析:(1)根据椭圆的标准方程,可知命题p为真命题时,-(m-6)>2m>0,解不等式组可得m的取值范围;
(2)根据双曲线的标准方程,可知命题q为真命题时,(m+1)•(m-1)<0,解不等式可得m的取值范围;
(3)若命题p或q为真命题,且命题p且q为假命题,则两个命题一真一假,结合(1)(2)的结论,分类讨论可得m的取值范围.
(2)根据双曲线的标准方程,可知命题q为真命题时,(m+1)•(m-1)<0,解不等式可得m的取值范围;
(3)若命题p或q为真命题,且命题p且q为假命题,则两个命题一真一假,结合(1)(2)的结论,分类讨论可得m的取值范围.
解答:解:(1)据椭圆的标准方程可得:
命题p为真命题时,-(m-6)>2m>0,
解之得0<m<2;
故命题p为真命题时m的取值范围为(0,2);…(4分)
(2)根据双曲线的标准方程,
若命题q为真命题,则(m+1)(m-1)<0,
解得-1<m<1,
故命题q为假命题时m的取值范围(-∞,-1]∪[1,+∞);…(9分)
(3)由题意,命题p与q一真一假,
当p真q假时有
解得1≤m<2
当p假q真时有
解得-1<m≤0
综上m的取值范围是(-1,0]∪[1,2).…(14分)
命题p为真命题时,-(m-6)>2m>0,
解之得0<m<2;
故命题p为真命题时m的取值范围为(0,2);…(4分)
(2)根据双曲线的标准方程,
若命题q为真命题,则(m+1)(m-1)<0,
解得-1<m<1,
故命题q为假命题时m的取值范围(-∞,-1]∪[1,+∞);…(9分)
(3)由题意,命题p与q一真一假,
当p真q假时有
|
解得1≤m<2
当p假q真时有
|
解得-1<m≤0
综上m的取值范围是(-1,0]∪[1,2).…(14分)
点评:本题又命题的真假判断为载体考查了椭圆的标准方程和双曲线的标准方程,其中根据圆锥曲线方程的特点分别求出命题p,q为真时,参数m的取值范围是解答的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 在其定义域内为减函数;命题
在其定义域内为减函数;命题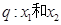 是方程
是方程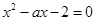 的两上实根,不等式
的两上实根,不等式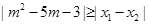 对任意实数
对任意实数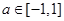 恒成立。
恒成立。 在其定义域内为减函数;命题q:x1和x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立.
在其定义域内为减函数;命题q:x1和x2是方程x2-ax-2=0的两个实根,不等式|m2-5m-3|≥|x1-x2|对任意实数a∈[-1,1]恒成立.