题目内容
据调查,湖南某地区有100万从事传统农业的农民,人均年收入3000元.为了增加农民的收入,当地政府积极引资建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作.据估计,如果有x(x>0)万人进入企业工作,那么剩下从事传统农业的农民的人均年收入有望提高2x%,而进入企业工作的农民人均年收入为3000a元(a>0为常数).(I)在建立加工企业后,要使该地区从事传统农业的农民的年总收入不低于加工企业建立前的年总收入,求x的取值范围;
(Ⅱ)在(I)的条件下,当地政府应安排多少万农民进入加工企业工作,才能使这100万农民的人均年收入达到最大?
【答案】分析:(I)先根据题意得出一个关于x的不等关系:(100-x)•3000•(1+2x%)≥100×3000,解此不等式即得x的取值范围;
(II)设这100万农民的人均年收入为y元,由题意得出函数y的解析式,下面分两类讨论:(1)若0<25(a+1)≤50,(2)若25(a+1)>50,分别求出它们的最大值即可.
解答:解:(I)据题意,(100-x)•3000•(1+2x%)≥100×3000,(2分)
即x2-50x≤0,解得0≤x≤50.(3分)
又x>0,故x的取值范围是(0,50].(4分)
(II)设这100万农民的人均年收入为y元,则
y=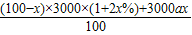 =
=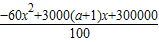
=- [x-25(a+1)]2+3000+475(a+1)2(0<x≤50).(9分)
[x-25(a+1)]2+3000+475(a+1)2(0<x≤50).(9分)
(1)若0<25(a+1)≤50,即0<a≤1,则当x=25(a+1)时,y取最大值;
(2)若25(a+1)>50,即a>1,则当x=50时,y取最大值.(11分)
答:当0<a≤1时,安排25(a+1)万人进入加工企业工作,当a>1时,
安排50万人进入企业工作,才能使这100万人的人均年收入最大.(13分)
点评:本小题主要考查函数模型的选择与应用,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.
(II)设这100万农民的人均年收入为y元,由题意得出函数y的解析式,下面分两类讨论:(1)若0<25(a+1)≤50,(2)若25(a+1)>50,分别求出它们的最大值即可.
解答:解:(I)据题意,(100-x)•3000•(1+2x%)≥100×3000,(2分)
即x2-50x≤0,解得0≤x≤50.(3分)
又x>0,故x的取值范围是(0,50].(4分)
(II)设这100万农民的人均年收入为y元,则
y=
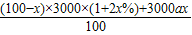 =
=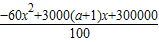
=-
 [x-25(a+1)]2+3000+475(a+1)2(0<x≤50).(9分)
[x-25(a+1)]2+3000+475(a+1)2(0<x≤50).(9分)(1)若0<25(a+1)≤50,即0<a≤1,则当x=25(a+1)时,y取最大值;
(2)若25(a+1)>50,即a>1,则当x=50时,y取最大值.(11分)
答:当0<a≤1时,安排25(a+1)万人进入加工企业工作,当a>1时,
安排50万人进入企业工作,才能使这100万人的人均年收入最大.(13分)
点评:本小题主要考查函数模型的选择与应用,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目