题目内容
判断正误:
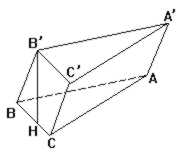
如图, 斜三棱柱ABC-A'B'C'的底面三角形ABC中, ∠C=90°, BC=2, B'在下底面的射影恰为BC中点H, 侧棱与底面夹角为60°, 侧面A'B'BA与侧面B'C'CB的夹角为30°, 则斜三棱柱的侧面积是6+2![]()
( )
体积是2![]()
(
)
答案:T;F
解析:
提示:
解析:
|
作CK⊥B'B于K , 连结AK, 由三垂线定理, B'B⊥AK. 所以∠AKC是二面角A-B'B-C平面角, 即∠AKC=30°, 且AKC是三棱柱的直截面. 在△B'BH中, 由∠BHB'=90°, ∠B'BH=60°, BH=1 可得B'B=2
在△BCK中, 由∠BKC=90°, ∠KBC=60°, BC=2可得KC=
在△ACK中, 由∠ACK=90°, ∠AKC=30°, KC=
|
提示:
|
1. 过AC作斜三棱柱的直截面KAC, 可先过C点作CK⊥BB'证明平面KAC就是直截面.
2. S侧等于直截面的周长与BB'的乘积
3. V等于直截面的面积与BB1的积.
|

练习册系列答案
相关题目