题目内容
设函数 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )A.把 的图象向左平移 的图象向左平移 个单位,得到一个偶函数的图象 个单位,得到一个偶函数的图象 |
B. 的图象关于点 的图象关于点 对称 对称 |
C. 的图象关于直线 的图象关于直线 对称 对称 |
D. 的最小正周期为 的最小正周期为 ,且在 ,且在 上为增函数 上为增函数 |
A
试题分析:根据正弦函数的性质可知f(x)=sin(2x+
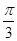 )的对称轴为2x+
)的对称轴为2x+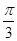 =kπ+
=kπ+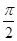 (k∈Z),即x=
(k∈Z),即x=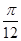 +
+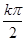 (k∈Z)∴直线x=
(k∈Z)∴直线x=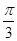 不是函数f(x)的对称轴,结论(3)错误
不是函数f(x)的对称轴,结论(3)错误根据正弦函数的性质可知f(x)=sin(2x+
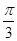 )的对称中心横坐标为2x+
)的对称中心横坐标为2x+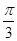 =kπ,即x=
=kπ,即x=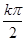 -
-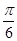 ,∴点(
,∴点(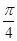 ,0)不是函数的对称中心.结论(2)错误.
,0)不是函数的对称中心.结论(2)错误.f(x)的图象向左平移
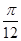 个单位,得f(x)=sin(2x+
个单位,得f(x)=sin(2x+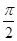 )
))=cos2x,为偶函数,∴结论(1)正确.
f(x)的最小正周期为π,且2kπ-
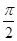 ≤2x+
≤2x+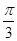 ≤2kπ+
≤2kπ+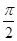 时,即kπ-
时,即kπ-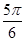 ≤x≤kπ+
≤x≤kπ+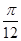
函数单调增,∴结论(4)不正确.故答案为A
点评:解决该试题的关键是利用正弦函数的单调性,对称性和三角函数图象的平移法则,对四个结论逐一验证,答案可得.

练习册系列答案
相关题目
 (
( ,
, 图像上一个最低点
图像上一个最低点 .
. 的解析式;
的解析式; 求
求 的值.
的值. 的图象只需将y=3sin2x的图象( )
的图象只需将y=3sin2x的图象( ) 个单位
个单位 个单位
个单位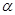 为第三象限角,则
为第三象限角,则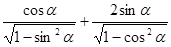 的值为 ( )
的值为 ( ) ,则
,则 的值为( )
的值为( )

 ,且
,且 满足
满足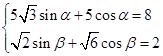
 的值.
的值. 的值.
的值.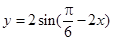 (
(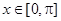 )的单调递增区间是( ).
)的单调递增区间是( ).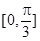
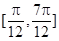
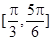
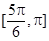
 的值( )
的值( )

 的内角
的内角 满足
满足 ,则
,则 ( )
( )


