题目内容
已知等差数列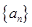 中,
中,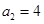 ;
;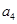 是
是 与
与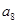 的等比中项.
的等比中项.
(I)求数列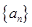 的通项公式:
的通项公式:
(II)若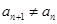 .求数列
.求数列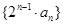 的前
的前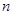 项和.
项和.
【答案】
(I)当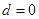 时,
时,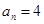 ;当
;当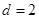 时,
时,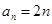 ;(II)
;(II)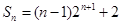 .
.
【解析】
试题分析:(I)通过已知 ,可以设公差为
,可以设公差为 ,然后根据等比中项的概念列出等式
,然后根据等比中项的概念列出等式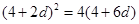 解出公差
解出公差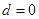 或
或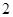 ,所以当
,所以当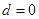 时,
时,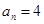 ;当
;当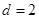 时,
时,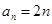 ;(II)根据条件可以确定
;(II)根据条件可以确定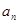 的通项公式
的通项公式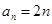 ,则
,则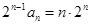 ,然后用错位相减法解出
,然后用错位相减法解出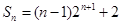 .
.
试题解析:(I)由题意, ,即
,即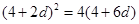 ,化简得
,化简得
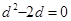 ,∴
,∴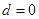 或
或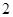
∵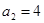 ,∴当
,∴当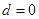 时,
时,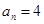 ;当
;当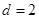 时,
时,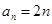 .
.
(II)∵ ,∴
,∴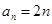 ,∴
,∴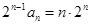 ,∴
,∴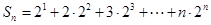 ……①
……①
①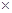 2,得
2,得 ……②,①-②,得
……②,①-②,得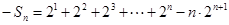 =
= ,∴
,∴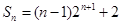 .
.
考点:1.等比中项的用法;2.错位相减法求数列和.

练习册系列答案
相关题目
 中,
中,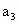 、
、 是方程
是方程 的两根,则
的两根,则 ________.
________. 中,
中,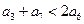 且
且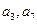 是方程
是方程 的两根,数列
的两根,数列 的前项和
的前项和 .
.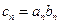 ,求数列
,求数列 的前
的前 项的和
项的和 ,并证明
,并证明
 中,
中, 且
且 是方程
是方程 的两根,数列
的两根,数列 的前项和
的前项和 .
. ,求数列
,求数列 的前
的前 项的和
项的和 ,并证明
,并证明
 中,Sn是前n项和,若S16>0且S17<0,则当Sn最大时,n的值为
中,Sn是前n项和,若S16>0且S17<0,则当Sn最大时,n的值为