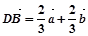题目内容
下列命题中:①y=2x与y=log2x互为反函数,其图象关于直线y=x对称;
②已知函数f(x-1)=x2-2x+1.,则f(5)=26;
③当a>0且a≠1时,函数f(x)=ax-2-3必过定点(2,-2);
④函数
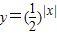 的值域是(0,+∞);
的值域是(0,+∞);上述命题中的所有正确命题的序号是 .
【答案】分析:根据同底的指数函数和对数函数互为反函数,可判断①正确;
根据x=6时,f(5)=25,可判断②错误;
根据x=2时,ax-2-3=-2恒成立,可判断③正确;
根据函数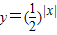 在x=0时取最小值1,可判断④错误;
在x=0时取最小值1,可判断④错误;
解答:解:根据同底的指数函数和对数函数互为反函数,图象关于原点对称,可判断①正确;
已知函数f(x-1)=x2-2x+1.令x=6,可得f(5)=25,故②错误;
当x=2时,ax-2-3=-2恒成立,故当a>0且a≠1时,函数f(x)=ax-2-3必过定点(2,-2),即③正确;
函数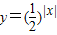 在x=0时取最小值1,故函数
在x=0时取最小值1,故函数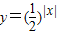 的值域是[1,+∞),故④错误;
的值域是[1,+∞),故④错误;
故答案为:①③
点评:本题又命题的真假判断为载体考查了反函数,函数求值,指数函数的图象和性质,是函数与逻辑的简单应用,难度中档.
根据x=6时,f(5)=25,可判断②错误;
根据x=2时,ax-2-3=-2恒成立,可判断③正确;
根据函数
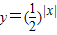 在x=0时取最小值1,可判断④错误;
在x=0时取最小值1,可判断④错误;解答:解:根据同底的指数函数和对数函数互为反函数,图象关于原点对称,可判断①正确;
已知函数f(x-1)=x2-2x+1.令x=6,可得f(5)=25,故②错误;
当x=2时,ax-2-3=-2恒成立,故当a>0且a≠1时,函数f(x)=ax-2-3必过定点(2,-2),即③正确;
函数
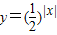 在x=0时取最小值1,故函数
在x=0时取最小值1,故函数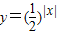 的值域是[1,+∞),故④错误;
的值域是[1,+∞),故④错误;故答案为:①③
点评:本题又命题的真假判断为载体考查了反函数,函数求值,指数函数的图象和性质,是函数与逻辑的简单应用,难度中档.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
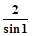 ;
;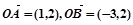 , O为坐标原点,则
, O为坐标原点,则 在
在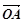 方向上的投影是
方向上的投影是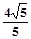 ;
;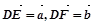 ,则
,则