题目内容
方程log2(x-1)=log4(3-x)的解集为
{2}
{2}
.分析:已知方程log2(x-1)=log4(3-x),分别画出函数f(x)=log2(x-1),g(x)=log4(3-x),利用数形结合的方法进行求解;
解答:解:∵方程log2(x-1)=log4(3-x),
∴令f(x)=log2(x-1),g(x)=log4(3-x),分别画出f(x)和g(x)的图象,交点即为解集,
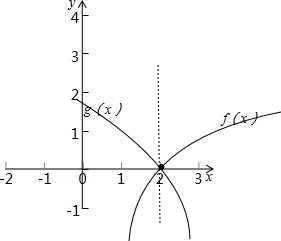
交点为(2,0),
∴方程的解集为{2},
故答案为{2}.
∴令f(x)=log2(x-1),g(x)=log4(3-x),分别画出f(x)和g(x)的图象,交点即为解集,

交点为(2,0),
∴方程的解集为{2},
故答案为{2}.
点评:此题主要考查对数函数的图象及其性质,利用了数形结合的方法,此题是一道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目