题目内容
设数列{an}、{bn}满足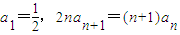 ,且
,且 ,n∈N*.
,n∈N*.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)对一切n∈N*,证明
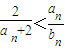 成立;
成立;(Ⅲ)记数列{an2}、{bn}的前n项和分别是An、Bn,证明:2Bn-An<4.
【答案】分析:(Ⅰ)由2nan+1=(n+1)an,得 ,由此可求出数列{an}的通项公式.
,由此可求出数列{an}的通项公式.
(Ⅱ)由 ,知要证明
,知要证明 ,只需证明ln(1+an)-an<0成立.构造函数f(x)=ln(1+x)-x(x≥0),则
,只需证明ln(1+an)-an<0成立.构造函数f(x)=ln(1+x)-x(x≥0),则 ,当x>0时,f'(x)<0,故f(x)<f(0)=0.ln(1+an)-an<0对一切n∈N*都成立.
,当x>0时,f'(x)<0,故f(x)<f(0)=0.ln(1+an)-an<0对一切n∈N*都成立.
(Ⅲ)由2bn-an2=2ln(1+an)<2an,知 ,利用错位相减求得2Bn-An<4.
,利用错位相减求得2Bn-An<4.
解答:解:(Ⅰ)由2nan+1=(n+1)an,得 ,(1分)
,(1分)
即数列 是以
是以 为首项,以
为首项,以 为公比的等比数列,∴
为公比的等比数列,∴ (3分)
(3分)
(Ⅱ)∵ ,
,
∴要证明 ,只需证明2bn<an2+2an,
,只需证明2bn<an2+2an,
即证 ,即证明ln(1+an)-an<0成立.(5分)
,即证明ln(1+an)-an<0成立.(5分)
构造函数f(x)=ln(1+x)-x(x≥0),(6分)
则 ,当x>0时,f'(x)<0,即f(x)在(0,+∞)上单调递减,
,当x>0时,f'(x)<0,即f(x)在(0,+∞)上单调递减,
故f(x)<f(0)=0.∴ln(1+x)-x<0,即ln(1+an)-an<0对一切n∈N*都成立,
∴ .(8分)
.(8分)
(Ⅲ)∵2bn-an2=2ln(1+an),由(Ⅱ)可知,2bn-an2=2ln(1+an)<2an,
∴2Bn-An<2(a1+a2++an)=2 (10分)
(10分)
利用错位相减求得: ,∴2Bn-An<4(12分)
,∴2Bn-An<4(12分)
点评:本题考查数列的性质和应用,解题时要注意构造和错位相减法的合理运用.
 ,由此可求出数列{an}的通项公式.
,由此可求出数列{an}的通项公式.(Ⅱ)由
 ,知要证明
,知要证明 ,只需证明ln(1+an)-an<0成立.构造函数f(x)=ln(1+x)-x(x≥0),则
,只需证明ln(1+an)-an<0成立.构造函数f(x)=ln(1+x)-x(x≥0),则 ,当x>0时,f'(x)<0,故f(x)<f(0)=0.ln(1+an)-an<0对一切n∈N*都成立.
,当x>0时,f'(x)<0,故f(x)<f(0)=0.ln(1+an)-an<0对一切n∈N*都成立.(Ⅲ)由2bn-an2=2ln(1+an)<2an,知
 ,利用错位相减求得2Bn-An<4.
,利用错位相减求得2Bn-An<4.解答:解:(Ⅰ)由2nan+1=(n+1)an,得
 ,(1分)
,(1分)即数列
 是以
是以 为首项,以
为首项,以 为公比的等比数列,∴
为公比的等比数列,∴ (3分)
(3分)(Ⅱ)∵
 ,
,∴要证明
 ,只需证明2bn<an2+2an,
,只需证明2bn<an2+2an,即证
 ,即证明ln(1+an)-an<0成立.(5分)
,即证明ln(1+an)-an<0成立.(5分)构造函数f(x)=ln(1+x)-x(x≥0),(6分)
则
 ,当x>0时,f'(x)<0,即f(x)在(0,+∞)上单调递减,
,当x>0时,f'(x)<0,即f(x)在(0,+∞)上单调递减,故f(x)<f(0)=0.∴ln(1+x)-x<0,即ln(1+an)-an<0对一切n∈N*都成立,
∴
 .(8分)
.(8分)(Ⅲ)∵2bn-an2=2ln(1+an),由(Ⅱ)可知,2bn-an2=2ln(1+an)<2an,
∴2Bn-An<2(a1+a2++an)=2
 (10分)
(10分)利用错位相减求得:
 ,∴2Bn-An<4(12分)
,∴2Bn-An<4(12分)点评:本题考查数列的性质和应用,解题时要注意构造和错位相减法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目