题目内容
如图四棱锥P—ABCD,PD⊥平面ABCD,PA与平面ABCD成60°角,在四边形ABCD中,∠D=∠DAB=90°,AB=4,CD=1,AD=2.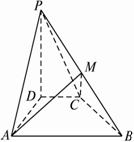
(1)若PB中点为M,求证平面AMC⊥平面PBC;
(2)求异面直线PA与BC所成的角.
解法一:(1)∵PA=2AD=4,PA=AB=4,M为PB的中点,?
∴AM⊥PB,PD=2![]() ,PC=
,PC=![]() =BC,?
=BC,?
∴CM⊥PB,AM∩CM=M,?
∴PB⊥面AMC,?
∴面AMC⊥面PBC.?
(2)过点A作AE平行于BC交CD的延长线于E点,连PE.AE=BC=![]() ,PA=4,PE=
,PA=4,PE=![]() ,
,
cos∠PAE=![]() =
=![]() ,所以异面直线PA与BC所成的角为arccos
,所以异面直线PA与BC所成的角为arccos![]() .
.
解法二:建立空间直角坐标系,以D点为原点,以DA所在直线为x轴,以DC所在直线为y轴,以DP所在直线为z轴.?
(1)M(1,2,![]() ),B(2,4,0),
),B(2,4,0),![]() =(-1,2,
=(-1,2,![]() ),
),![]() =(1,1,
=(1,1,![]() ),
),![]() =(2,4,-2
=(2,4,-2![]() ),
),
∴![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
∴面AMC⊥面PBC.?
(2)![]() =(2,0,-2
=(2,0,-2![]() ),
),![]() =(-2,-3,0,),cos〈
=(-2,-3,0,),cos〈![]() ,
,![]() 〉=-
〉=-![]() .?
.?
∴异面直线PA与BC所成的角为arccos![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
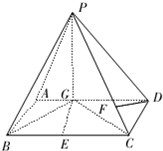 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且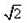 ,F是BC的中点.
,F是BC的中点.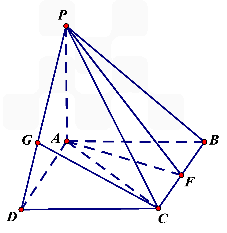
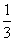 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.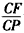 的值。
的值。 
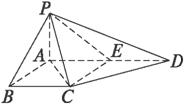
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.