题目内容
已知
，
是空间两个向量，若|
|=2，|
|=2，|
-
|=
，则cos＜
，
＞=
．
| a |
| b |
| a |
| b |
| a |
| b |
| 7 |
| a |
| b |
| 1 |
| 8 |
| 1 |
| 8 |
分析：将式子|
-
|=
平方可得
2-2
•
+
2=7，由数量积的定义，代入数据化简可得．
| a |
| b |
| 7 |
| a |
| a |
| b |
| b |
解答：解：将式子|
-
|=
平方可得
2-2
•
+
2=7，
故可得
2-2|
|•|
|cos＜
，
＞+
2=7，
代入数据可得cos＜
，
＞=
=
=
故答案为：
| a |
| b |
| 7 |
| a |
| a |
| b |
| b |
故可得
| a |
| a |
| b |
| a |
| b |
| b |
代入数据可得cos＜
| a |
| b |
| ||||
2|
|
| 22+22-7 |
| 2×2×2 |
| 1 |
| 8 |
故答案为：
| 1 |
| 8 |
点评：本题考查向量的夹角公式，涉及向量的数量积的运算，属中档题．
练习册系列答案
相关题目
α，b
a∥b
与圆
恒有公共点；
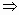为△ABC的内角，则
最小值为
；
}中，
则使其前n项和
成立的最大正整数为2013;