Question

已知函数方程f（x）=x³+bx²+cx+d（b，c，d为常数），当k∈（-∞，0）∪（4，+∞）时，方程f（x）-k=0有且仅有一个实根，当k∈（0，4）时，方程f（x）-k=0有3个相异实根．给出下列4个命题：
①方程f（x）=4和f'（x）=0有且仅有一个相同的实根；
②方程f（x）=0和f'（x）=0有且仅有一个相同的实根；
③方程f（x）+3=0的任一实根都大于f（x）-1=0的任一实根；
④方程f（x）+5=0的任一实根都小于f（x）-2=0的任一实根．
其中正确命题的序号是________．

Answer 1

①②④
分析：f（x）-k=0的根的问题可转化为f（x）=k，即y=k和y=f（x）图象交点个数问题．由题意y=f（x）图象应为先增后减再增，极大值为4，极小值为0．
解答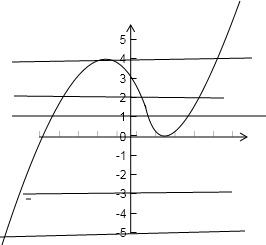：解：由题意y=f（x）图象应为先增后减再增，
极大值为4，极小值为0．
f（x）-k=0的根的问题可转化为f（x）=k，
即y=k和y=f（x）图象交点个数问题．
故答案为：①②④
点评：本题考查方程根的问题，方程根的问题?函数的零点问题?两个函数图象的交点问题，转化为数形结合求解．