题目内容
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=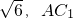 =3,AB=2,BC=1.
=3,AB=2,BC=1.
(1)证明:BC⊥平面ACC1A1.
(2)D为CC1中点,在棱AB上是否存在一点E,使DE∥平面AB1C1,证明你的结论.
(3)求二面角B-AB1-C1的余弦值的大小.
(1)证明:在矩形ACC1A1中,AA1=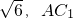 =3,AB=2,BC=1
=3,AB=2,BC=1
∴AB2=AC2+BC2
∴BC⊥AC
∵AA1⊥平面ABC,
∴AA1⊥BC
∵AA1∩AC=A
∴BC⊥平面ACC1A1;
(2)解:分别取BB1中点M和AB中点E,由DM∥B1C1,EM∥AB1,得平面EMD∥平面AB1C1,∴DE∥平面AB1C1,
即E为AB中点时,DE∥平面AB1C1;
(3)解:以C为坐标原点,CB,CC1,CA所在直线分别为x轴、y轴、z轴建立空间直角坐标系,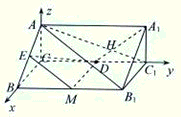
则C(0,0,0),B(1,0,0),A(0,0, ),C1(0,
),C1(0, ,0),B1(1,
,0),B1(1, ,0),A1(0,
,0),A1(0, ,
, ),D(0,
),D(0, ,0)
,0)
设 是平面ABB1的一个法向量
是平面ABB1的一个法向量
由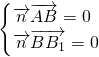 可得
可得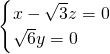 ,∴可取
,∴可取 =(
=(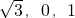 )
)
∵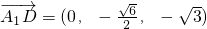 是平面AB1C1的一个法向量,且
是平面AB1C1的一个法向量,且 与二面角B-AB1-C1的大小相等
与二面角B-AB1-C1的大小相等
∴cos =
=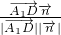 =-
=-
∴所求二面角B-AB1-C1的余弦值的大小为- .
.
分析:(1)先证明BC⊥AC,由AA1⊥平面ABC,可得AA1⊥BC,利用线面垂直的判定,可得结论;
(2)分别取BB1中点M和AB中点E,可得平面EMD∥平面AB1C1,从而DE∥平面AB1C1;
(3)建立空间直角坐标系,求出平面ABB1的一个法向量 =(
=(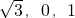 ),
),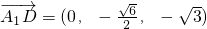 是平面AB1C1的一个法向量,且
是平面AB1C1的一个法向量,且 与二面角B-AB1-C1的大小相等,从而可求二面角B-AB1-C1的余弦值的大小.
与二面角B-AB1-C1的大小相等,从而可求二面角B-AB1-C1的余弦值的大小.
点评:本题主要考查二面角的计算,直线和平面垂直、平行的性质、判定,考查学生空间想象能力,计算能力、转化能力
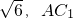 =3,AB=2,BC=1
=3,AB=2,BC=1∴AB2=AC2+BC2
∴BC⊥AC
∵AA1⊥平面ABC,
∴AA1⊥BC
∵AA1∩AC=A
∴BC⊥平面ACC1A1;
(2)解:分别取BB1中点M和AB中点E,由DM∥B1C1,EM∥AB1,得平面EMD∥平面AB1C1,∴DE∥平面AB1C1,
即E为AB中点时,DE∥平面AB1C1;
(3)解:以C为坐标原点,CB,CC1,CA所在直线分别为x轴、y轴、z轴建立空间直角坐标系,

则C(0,0,0),B(1,0,0),A(0,0,
 ),C1(0,
),C1(0, ,0),B1(1,
,0),B1(1, ,0),A1(0,
,0),A1(0, ,
, ),D(0,
),D(0, ,0)
,0)设
 是平面ABB1的一个法向量
是平面ABB1的一个法向量由
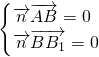 可得
可得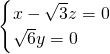 ,∴可取
,∴可取 =(
=(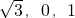 )
)∵
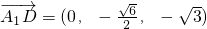 是平面AB1C1的一个法向量,且
是平面AB1C1的一个法向量,且 与二面角B-AB1-C1的大小相等
与二面角B-AB1-C1的大小相等∴cos
 =
=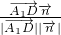 =-
=-
∴所求二面角B-AB1-C1的余弦值的大小为-
 .
.分析:(1)先证明BC⊥AC,由AA1⊥平面ABC,可得AA1⊥BC,利用线面垂直的判定,可得结论;
(2)分别取BB1中点M和AB中点E,可得平面EMD∥平面AB1C1,从而DE∥平面AB1C1;
(3)建立空间直角坐标系,求出平面ABB1的一个法向量
 =(
=(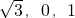 ),
),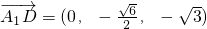 是平面AB1C1的一个法向量,且
是平面AB1C1的一个法向量,且 与二面角B-AB1-C1的大小相等,从而可求二面角B-AB1-C1的余弦值的大小.
与二面角B-AB1-C1的大小相等,从而可求二面角B-AB1-C1的余弦值的大小.点评:本题主要考查二面角的计算,直线和平面垂直、平行的性质、判定,考查学生空间想象能力,计算能力、转化能力

练习册系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=