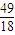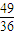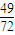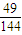题目内容
曲线y=x3-x2在点P(2,4)处的切线方程为
8x-y-12=0
8x-y-12=0
.分析:由求导公式和法则求出导数,再把x=2代入求出切线的斜率,再代入点斜式方程化为一般式即可.
解答:解:由题意得,y′=3x2-2x,
则点P(2,4)处的切线斜率k=12-4=8,
∴点P(2,4)处的切线方程是:y-4=8(x-2),
即8x-y-12=0,
故答案为:8x-y-12=0.
则点P(2,4)处的切线斜率k=12-4=8,
∴点P(2,4)处的切线方程是:y-4=8(x-2),
即8x-y-12=0,
故答案为:8x-y-12=0.
点评:本题考查了导数的几何意义,即某点处的切线的斜率是该点出的导数值,以及点斜式方程的应用.

练习册系列答案
相关题目
 x3+
x3+ x2在点T(1,
x2在点T(1, )处的切线与两坐标轴围成的三角形的面积为( )
)处的切线与两坐标轴围成的三角形的面积为( )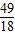
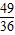
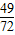
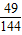
 x3+
x3+ x2在点T(1,
x2在点T(1, )处的切线与两坐标轴围成的三角形的面积为( )
)处的切线与两坐标轴围成的三角形的面积为( )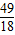

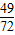
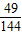
 x3+
x3+ x2在点T(1,
x2在点T(1, )处的切线与两坐标轴围成的三角形的面积为( )
)处的切线与两坐标轴围成的三角形的面积为( )