题目内容
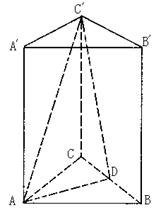
如图,在正三棱柱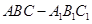 中,
中,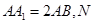 是
是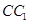 的中点,
的中点,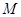 是线段
是线段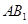 上的动点,且
上的动点,且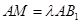
(1)若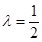 ,求证:
,求证: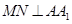 ;
;
(2) 求二面角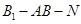 的余弦值;
的余弦值;
(3) 若直线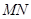 与平面
与平面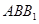 所成角的大小为
所成角的大小为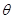 ,求
,求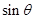 的最大值.
的最大值.
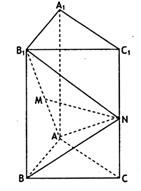
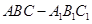 中,
中,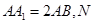 是
是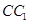 的中点,
的中点,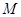 是线段
是线段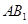 上的动点,且
上的动点,且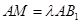
(1)若
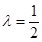 ,求证:
,求证: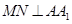 ;
;(2) 求二面角
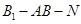 的余弦值;
的余弦值;(3) 若直线
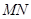 与平面
与平面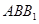 所成角的大小为
所成角的大小为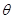 ,求
,求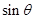 的最大值.
的最大值.
解析:(1)证明:取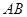 中点
中点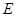 ,连接
,连接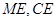 ,则有
,则有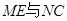 平行且相等
平行且相等
所以四边形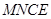 是平行四边形,
是平行四边形,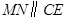 ……………..2分
……………..2分
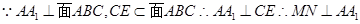 ……………..3分
……………..3分
(2)设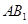 中点为
中点为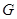 ,连接
,连接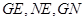
则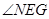 即为所求二面角的平面角
即为所求二面角的平面角
又易得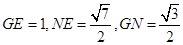 …………………………………..5分
…………………………………..5分
由余弦定理得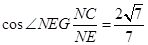 ……………………………..7分
……………………………..7分
另法:以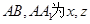 轴,在面
轴,在面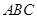 内以过
内以过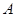 点且垂直于
点且垂直于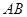 的射线为
的射线为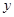 轴建系如图,设
轴建系如图,设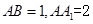 ,则
,则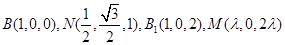
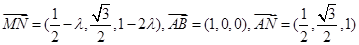 …………………………..5分
…………………………..5分
设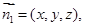 是平面
是平面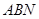 的一个法向量,则
的一个法向量,则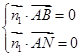
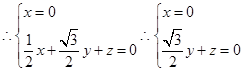
令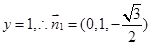 ……………………..7分
……………………..7分
设二面角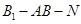 的大小为
的大小为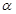 ,又平面
,又平面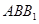 的法向量
的法向量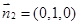
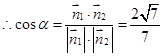 ……………………..8分
……………………..8分
(3)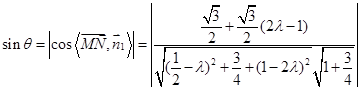
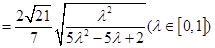 …………………..10分
…………………..10分
令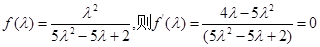
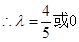 .
.
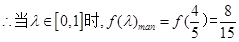
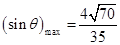 …………………………………………..12分
…………………………………………..12分
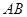 中点
中点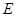 ,连接
,连接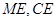 ,则有
,则有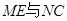 平行且相等
平行且相等所以四边形
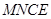 是平行四边形,
是平行四边形,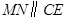 ……………..2分
……………..2分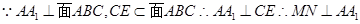 ……………..3分
……………..3分(2)设
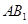 中点为
中点为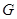 ,连接
,连接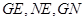
则
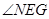 即为所求二面角的平面角
即为所求二面角的平面角又易得
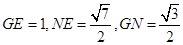 …………………………………..5分
…………………………………..5分由余弦定理得
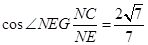 ……………………………..7分
……………………………..7分另法:以
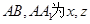 轴,在面
轴,在面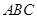 内以过
内以过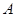 点且垂直于
点且垂直于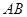 的射线为
的射线为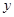 轴建系如图,设
轴建系如图,设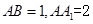 ,则
,则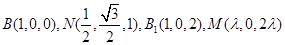
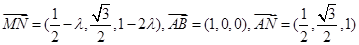 …………………………..5分
…………………………..5分设
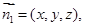 是平面
是平面 的一个法向量,则
的一个法向量,则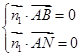
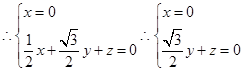
令
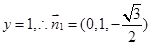 ……………………..7分
……………………..7分设二面角
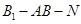 的大小为
的大小为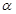 ,又平面
,又平面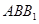 的法向量
的法向量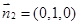
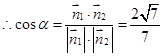 ……………………..8分
……………………..8分(3)
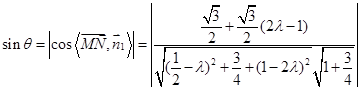
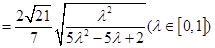 …………………..10分
…………………..10分令
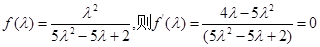
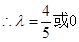 .
.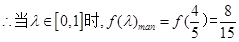
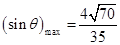 …………………………………………..12分
…………………………………………..12分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
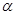 、
、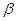 是两个不同的平面,则下列说法正确的是
是两个不同的平面,则下列说法正确的是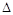 ABC
ABC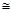
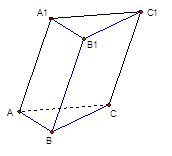
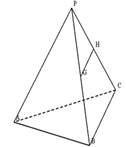
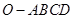 中,底面
中,底面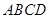 为菱形,
为菱形,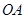 ⊥平面
⊥平面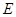 为
为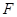 为
为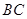 的中点,求证:(Ⅰ)平面
的中点,求证:(Ⅰ)平面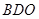 ⊥平面
⊥平面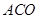 ;(Ⅱ)
;(Ⅱ)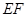 //平面
//平面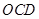 .
.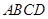 是矩形,
是矩形,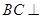 平面
平面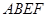 ,四边形
,四边形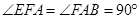 ,
,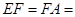
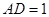 ,点
,点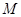 是
是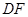 的中点,
的中点,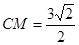 .
.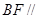 平面
平面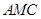 ;
;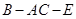 的余弦值.
的余弦值. 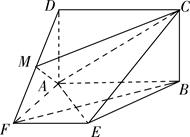
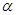 、
、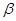 是空间不同的平面,a、b是空间不同的直线,下列命题错误的是( )
是空间不同的平面,a、b是空间不同的直线,下列命题错误的是( )

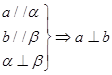
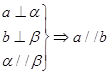
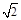 ,AB=1,E是DD1的中点。
,AB=1,E是DD1的中点。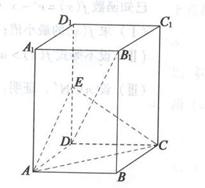
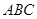 —
—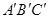 中,点D是BC的中点,欲过点
中,点D是BC的中点,欲过点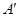 作一截面与平面
作一截面与平面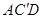 平行,问应当怎样画线,并说明理由。
平行,问应当怎样画线,并说明理由。