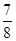题目内容
已知函数f(x)=2sinx•cos2
+cosx•sinθ-sinx(0<θ<π)在x=π处取最小值.
(1)求θ的值;
(2)在△ABC中,a,b,c分别为角A,B,C的对边,已知a=1,b=
,f(A)=
,求角C.
| θ |
| 2 |
(1)求θ的值;
(2)在△ABC中,a,b,c分别为角A,B,C的对边,已知a=1,b=
| 2 |
| ||
| 2 |
(1)f(x)=2sinx•
+cosx•sinθ-sinx=sin(x+θ)
∵当x=π时,f(x)取得最小值
∴sin(π+θ)=-1即sinθ=1
又∵0<θ<π,
∴θ=
(2)由(1)知f(x)=cosx
∵f(A)=cosA=
,且A为△ABC的内角∴A=
由正弦定理得sinB=
=
知B=
或B=
当B=
时,C=π-A-B=
,
当B=
时,C=π-A-B=
综上所述,C=
或C=
| 1+cosθ |
| 2 |
∵当x=π时,f(x)取得最小值
∴sin(π+θ)=-1即sinθ=1
又∵0<θ<π,
∴θ=
| π |
| 2 |
(2)由(1)知f(x)=cosx
∵f(A)=cosA=
| ||
| 2 |
| π |
| 6 |
由正弦定理得sinB=
| bsinA |
| a |
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |
当B=
| π |
| 4 |
| 7π |
| 12 |
当B=
| 3π |
| 4 |
| π |
| 12 |
综上所述,C=
| 7π |
| 12 |
| π |
| 12 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
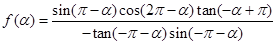
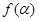 ;
;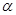 是第三象限角,且cos(
是第三象限角,且cos(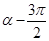 )=
)=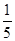 ,求
,求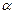 的顶点在原点,始边与
的顶点在原点,始边与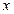 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点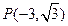
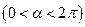 .
.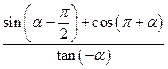 的值;
的值;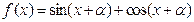 (
(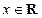 )的图像关于直线
)的图像关于直线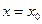 对称,求
对称,求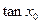 的值.
的值.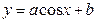 的最大值为1,最小值为-3,试确定
的最大值为1,最小值为-3,试确定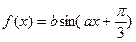 的
的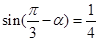 ,则
,则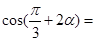 ( )
( )