题目内容
给出下列三个命题:①k=±1是直线y=k(x+1)与抛物线y2=4x只有一个交点的充要条件
②函数f(x)=lnx-
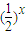 在x∈(1,e)上有且只有一个零点
在x∈(1,e)上有且只有一个零点③直线ax+y+2a=0与圆x2+2x+y2-3=0恒有两个不同交点.
其中不正确的命题序号是 .
【答案】分析:由直线与抛物线的关系,我们求出直线y=k(x+1)与抛物线y2=4x只有一个交点时,参数k的取值,结合充要条件的定义,我们可以判断①的真假;由函数零点个数的判断方法,我们可以判断②的真假;根据直线与圆的位置关系判断方法,我们可以判断出③的真假,进而得到答案.
解答:解:∵k=0时,直线y=k(x+1)与抛物线y2=4x也只有一个交点,故k=±1是直线y=k(x+1)与抛物线y2=4x只有一个交点的充分不必要条件,故①错误;
函数f(x)=lnx-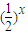 在区间(1,e)上单调递增,且f(0)•f(e)<0,故函数f(x)=lnx-
在区间(1,e)上单调递增,且f(0)•f(e)<0,故函数f(x)=lnx- 在x∈(1,e)上有且只有一个零点正确;
在x∈(1,e)上有且只有一个零点正确;
直线ax+y+2a=0恒过(-2,0)点,而(-2,0)点在圆x2+2x+y2-3=0内,故直线ax+y+2a=0与圆x2+2x+y2-3=0恒有两个不同交点正确;
故答案为①
点评:本题考查的知识点是命题的真假判断,函数的零点,直线与圆的位置关系,直线与圆锥曲线的位置关系,其中根据上述基本知识点判断出题目中三个命题的真假是解答本题的关键,①中易忽略直线与抛物线的对称轴平行的情况.
解答:解:∵k=0时,直线y=k(x+1)与抛物线y2=4x也只有一个交点,故k=±1是直线y=k(x+1)与抛物线y2=4x只有一个交点的充分不必要条件,故①错误;
函数f(x)=lnx-
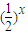 在区间(1,e)上单调递增,且f(0)•f(e)<0,故函数f(x)=lnx-
在区间(1,e)上单调递增,且f(0)•f(e)<0,故函数f(x)=lnx- 在x∈(1,e)上有且只有一个零点正确;
在x∈(1,e)上有且只有一个零点正确;直线ax+y+2a=0恒过(-2,0)点,而(-2,0)点在圆x2+2x+y2-3=0内,故直线ax+y+2a=0与圆x2+2x+y2-3=0恒有两个不同交点正确;
故答案为①
点评:本题考查的知识点是命题的真假判断,函数的零点,直线与圆的位置关系,直线与圆锥曲线的位置关系,其中根据上述基本知识点判断出题目中三个命题的真假是解答本题的关键,①中易忽略直线与抛物线的对称轴平行的情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目