题目内容
如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中以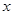 表示.
表示.
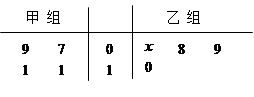
(1)如果乙组同学投篮命中次数的平均数为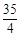 ,求
,求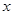 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为17的概率.
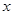 表示.
表示.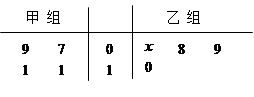
(1)如果乙组同学投篮命中次数的平均数为
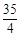 ,求
,求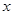 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为17的概率.
(1)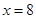 ,方差
,方差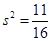 .(2)
.(2)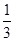 .
.
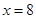 ,方差
,方差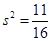 .(2)
.(2)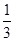 .
.试题分析:(1)由
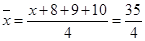 ,得
,得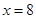 ,
,应用方差计算公式可得
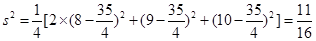 .
.(2)记甲组投篮命中次数低于10次的同学为
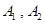 ,他们的命中次数分别为9,7.
,他们的命中次数分别为9,7.乙组投篮命中次数低于10次的同学为
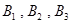 ,他们的命中次数分别为8,8,9.
,他们的命中次数分别为8,8,9.依题意,不同的选取方法有:
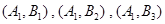 ,
, 共6种. 9分
共6种. 9分设“这两名同学的投篮命中次数之和为17”为事件C,则C中恰含有
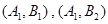 共2种.
共2种.由古典概型概率的计算公式可得.
试题解析:(1)依题意得:
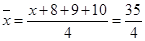 ,解得
,解得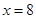 , 3分
, 3分方差
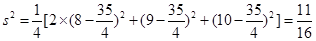 . 6分
. 6分(2)记甲组投篮命中次数低于10次的同学为
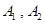 ,他们的命中次数分别为9,7.
,他们的命中次数分别为9,7.乙组投篮命中次数低于10次的同学为
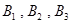 ,他们的命中次数分别为8,8,9.
,他们的命中次数分别为8,8,9.依题意,不同的选取方法有:
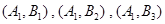 ,
, 共6种. 9分
共6种. 9分设“这两名同学的投篮命中次数之和为17”为事件C,则C中恰含有
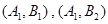 共2种.
共2种.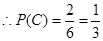 . 12分
. 12分
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
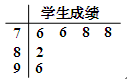
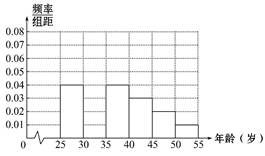
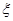 为这两位同学中成绩低于平均分的人数,求
为这两位同学中成绩低于平均分的人数,求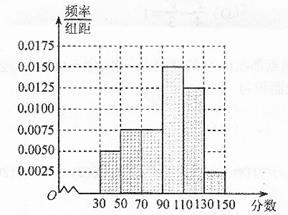
 ,求
,求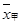 、
、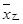 表示,则下列结论正确的是( )
表示,则下列结论正确的是( )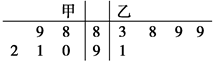
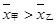 ,且甲比乙成绩稳定
,且甲比乙成绩稳定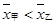 ,且甲比乙成绩稳定
,且甲比乙成绩稳定