题目内容
((本题14分)如图4,已知椭圆 的离心率为
的离心率为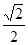 ,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4
,以该椭圆上的点和椭圆的左右焦点F1,F2为顶点的三角形的周长为4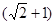 。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
。一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D。
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线PF1、PF2的斜率分别为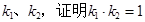 ;
;
(Ⅲ)是否存在常数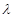 ,使得
,使得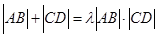 恒成立?若存在,求
恒成立?若存在,求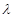 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。

【答案】
解:(Ⅰ)由题意知,椭圆离心率为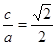 ,得
,得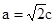 ,又
,又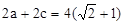 ,
,
∴可解得 ,∴
,∴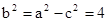 ,
,
∴椭圆的标准方程为;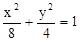 ;
…2分
;
…2分
∴椭圆的焦点坐标为(±2,0),因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,
∴该双曲线的标准方程为 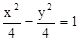 …4分
…4分
(Ⅱ)设点P(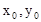 ),则
),则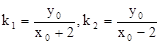 ,
,
∴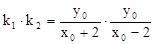
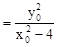 ,
…6分
,
…6分
又点P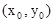 在双曲线上,∴有
在双曲线上,∴有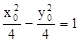 ,即
,即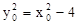 ,
,
∴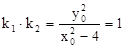 。
…8分
。
…8分
(Ⅲ)假设存在常数λ,使得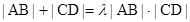 恒成立,则由(Ⅱ)知
恒成立,则由(Ⅱ)知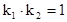 ,
,
∴设直线AB的方程为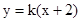 ,则直线CD的方程为
,则直线CD的方程为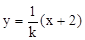 ,
,
由方程组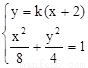 消y得:
消y得: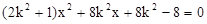 ,…10分
,…10分
设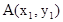 ,B(
,B(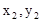 ),
),
则由韦达定理得: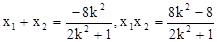 ,
,
∴ ,同理可得
,同理可得

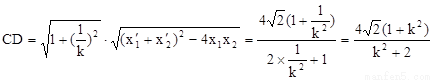 ,…12分
,…12分
又∵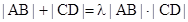 ,
,
∴有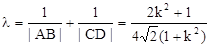 -
-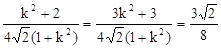 ,
,
∴存在常数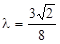 ,使得
,使得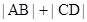 =
=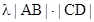 恒成立。
…14分
恒成立。
…14分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,
如图,

 中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点
中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点