Question

【题目】两个单位向量 ， 的夹角为60°，点C在以O圆心的圆弧AB上移动， =x +y ，则x+y的最大值为（ ）
A.1
B.
C.
D.

Answer 1

【答案】D
【解析】解：∵两个单位向量 ， 的夹角为60°，点C在以O圆心的
圆弧AB上移动， =x +y ，
建立如图所示的坐标系，则B（1，0），A（cos60°，sin60°），
即A（ ， ）．
设∠BOC=α，则 =x +y =（cosα，sinα）=（ x+y， x），
∴ ∴x= sinα，y=cosα﹣ sinα，
∴x+y=cosα+ sinα= sin（α+60°）．
∵0°≤α≤60°，∴60°≤α+60°≤120°，∴ ≤sin（α+60°）≤1，
故当α+60°=90°时，x+y取得最大值为 ，
故选：D．

【考点精析】通过灵活运用基本不等式和数量积表示两个向量的夹角，掌握基本不等式：,（当且仅当时取到等号）；变形公式：；设、都是非零向量，，，是与的夹角，则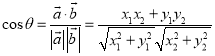即可以解答此题．