题目内容
已知函数f(x)=log
(3+2x-x2).
(Ⅰ) 求函数f(x)的单调区间;
(Ⅱ) 求函数f(x)的值域.
| 1 | 2 |
(Ⅰ) 求函数f(x)的单调区间;
(Ⅱ) 求函数f(x)的值域.
分析:(Ⅰ)设t=3+2x-x2,则y=log
t.求出f(x)的定义域,先研究t,y的单调性,再根据复合函数单调性的判定方法即可求得f(x)的单调区间,注意定义域;
(Ⅱ)在f(x)的定义域内先求函数t=-(x-1)2+4的值域,再结合为y=log2t的单调性即可求得f(x)的值域;
| 1 |
| 2 |
(Ⅱ)在f(x)的定义域内先求函数t=-(x-1)2+4的值域,再结合为y=log2t的单调性即可求得f(x)的值域;
解答:解:(Ⅰ)设t=3+2x-x2,则y=log
t.
由t=3+2x-x2>0得x2-2x-3<0,即(x+1)(x-3)<0,解得-1<x<3.
因为t=-(x-1)2+4,所以抛物线的对称轴为x=1.
当x∈(-1,1]时,t是x的增函数,y是t的减函数;
当x∈[1,3)时,t是x的减函数,y是t的减函数.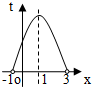
所以,函数f(x)的单调递增区间为[1,3),单调递减区间为(-1,1].
(Ⅱ)如图:
由(Ⅰ)知t=-(x-1)2+4,当x=1时,tmax=4.
又因为y=log2t在(0,4]上是减函数,
所以当tmax=4时,ymin=log
4=log
(
)-2=-2.
故函数f(x)的值域为[-2,+∞).
| 1 |
| 2 |
由t=3+2x-x2>0得x2-2x-3<0,即(x+1)(x-3)<0,解得-1<x<3.
因为t=-(x-1)2+4,所以抛物线的对称轴为x=1.
当x∈(-1,1]时,t是x的增函数,y是t的减函数;
当x∈[1,3)时,t是x的减函数,y是t的减函数.

所以,函数f(x)的单调递增区间为[1,3),单调递减区间为(-1,1].
(Ⅱ)如图:
由(Ⅰ)知t=-(x-1)2+4,当x=1时,tmax=4.
又因为y=log2t在(0,4]上是减函数,
所以当tmax=4时,ymin=log
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故函数f(x)的值域为[-2,+∞).
点评:本题考查复合函数的单调性、对数函数、二次函数的性质及函数值域的求解,属中档题,判断复合函数单调性的方法:“同增异减”.

练习册系列答案
相关题目