��Ŀ����
��֪P1��x1��y1����P2��x2��y2���Ǻ���f(x)=
ͼ���ϵ����㣬��
=
(
+
)����P��A��B���ߣ���
=x1
+x2
��1����P������
��2����S2011=
f(
)����S2011
��3����Sn=
f(
)����Tn����{
}ǰn��ĺͣ���Tn��a(Sn+1+
)ʱ����һ��n��N*������������a��ȡֵ��Χ��
| 2x | ||
2x+
|
| OP |
| 1 |
| 2 |
| OP1 |
| OP2 |
| CP |
| CA |
| CB |
��1����P������
��2����S2011=
| 2010 |
 |
| i=1 |
| i |
| 2011 |
��3����Sn=
| n |
 |
| i=1 |
| i |
| n |
| 1 | ||||
(Sn+
|
| 2 |
��������1����P��A��B������
=x1
+x2
������x1+x2=1�������֪��������ʽ��Ѱ��f��x����f��1-x���ĺ���ֵ�Ĺ�ϵ���Ӷ�����P
��2����ϣ�1����f��x����f��1-x���ĺ͵Ĺ�ϵ�����õ��������ͼ������
��3�����õ�����ӿ���Sn������֮������������ӿ���Tn����������a�ķ�Χ
| CP |
| CA |
| CB |
��2����ϣ�1����f��x����f��1-x���ĺ͵Ĺ�ϵ�����õ��������ͼ������
��3�����õ�����ӿ���Sn������֮������������ӿ���Tn����������a�ķ�Χ
����⣨1����P��A��B������
=x1
+x2
��
��x1+x2=1
�֡�f(x)+f(1-x)=
+
=
+
=1
��P(
��
)
��2��S2011=
f(
)=f(
)+f(
)+��+f(
)+f(
)
��S2011=f(
)+f(
)+��f(
)+f(
)
��2S2011=2010⇒S2011=1005
��3��Sn=
f(
)=f(
)+f(
)+��f(
)+f(1)
��Sn=f(1)+f(
)+��f(
)+f(
)
��Sn=
-
��bn=
=
��Tn=
��
��a
⇒a��
=
=
��a��
| CP |
| CA |
| CB |
��x1+x2=1
�֡�f(x)+f(1-x)=
| 2x | ||
2x+
|
| 21-x | ||
21-x+
|
| 2x | ||
2x+
|
| ||
2x+
|
��P(
| 1 |
| 2 |
| 1 |
| 2 |
��2��S2011=
| 2010 |
 |
| i=1 |
| i |
| 2011 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 2009 |
| 2011 |
| 2010 |
| 2011 |
��S2011=f(
| 2010 |
| 2011 |
| 2009 |
| 2011 |
| 2 |
| 2011 |
| 1 |
| 2011 |
��2S2011=2010⇒S2011=1005
��3��Sn=
| n |
 |
| i=1 |
| i |
| n |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
��Sn=f(1)+f(
| n-1 |
| n |
| 2 |
| n |
| 1 |
| n |
��Sn=
| n+3 |
| 2 |
| 2 |
��bn=
| 1 | ||||
(Sn+
|
| 4 |
| (n+3)(n+4) |
��Tn=
| 2n |
| n+2 |
| 2n |
| n+2 |
| n+2 |
| 2 |
| 4n |
| (n+2)2 |
| 4n |
| n2+4n+4 |
| 4 | ||
n+
|
��a��
| 1 |
| 8 |
������������Ҫ��������������������Ӧ�ü�������ӡ�������ͷ�����Ӧ�ã������������뺯��֪ʶ���ۺ�Ӧ��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
��֪P1��x1��y1����P2��x2��y2����ֱ��ax+by+c=0��b��0���ϵ����㣬��P1P2�ij��ǣ�������
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
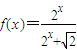 ͼ���ϵ����㣬��
ͼ���ϵ����㣬��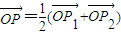 ����P��A��B���ߣ���
����P��A��B���ߣ���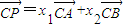
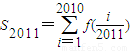 ����S2011
����S2011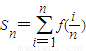 ����Tn����
����TnΪ����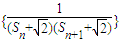 ǰn��ĺͣ���
ǰn��ĺͣ���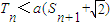 ʱ����һ��n��N*������������a��ȡֵ��Χ��
ʱ����һ��n��N*������������a��ȡֵ��Χ��