题目内容

（2011•南通一模）选修4-5：不等式选讲
设n∈N*，求证：
C
1
n
+
C
2
n
+…+
C
n
n
≤
n(2n-1)
．
分析：要证原结论成立，只需证两端平方后的式子成立即可，左端利用基本不等式放缩后，整理即可证得．
解答：证明：要证
C
1
n
+
C
2
n
+…+
C
n
n
≤
n(2n-1)
，
只需证两端平方后的式子成立，
即证
C
1
n
+
C
2
n
+…+
C
n
n
+2
C
1
n
•
C
2
n
+2
C
1
n
•
C
3
n
+…+2
C
1
n
•
C
n
n
+2
C
2
n
•
C
3
n
+2
C
2
n
•
C
4
n
+…+2
C
n-1
n
•
C
n
n
≤n（2n-1）成立．
而左端=
C
1
n
+
C
2
n
+…+
C
n
n
+2
C
1
n
•（
C
2
n
+
C
3
n
+…+
C
n
n
）+2
C
2
n
（
C
3
n
+
C
4
n
+…+
C
n
n
）+…+2
C
n-1
n
•
C
n
n

≤
C
1
n
+
C
2
n
+…+
C
n
n
+[（
C
1
n
+
C
2
n
）+（
C
1
n
+
C
3
n
）+…+（
C
1
n
+
C
n
n
）]+[（
C
2
n
+
C
3
n
）+（
C
2
n
+
C
4
n
）+…+（
C
2
n
+
C
n
n
）]+…+（
C
n-1
n
+
C
n
n
）
=
C
1
n
+
C
2
n
+…+
C
n
n
+（n-1）
C
1
n
+（n-1）
C
2
n
+（n-1）
C
3
n
+…+（n-1）
C
n
n

=
C
1
n
+
C
2
n
+…+
C
n
n
+（n-1）（
C
1
n
+
C
2
n
+…+
C
n
n
）
=n（
C
1
n
+
C
2
n
+…+
C
n
n
）
=n（
C
0
n
+
C
1
n
+
C
2
n
+…+
C
n
n
-
C
0
n
）
=n（2n-1）成立．
∴原不等式
C
1
n
+
C
2
n
+…+
C
n
n
≤
n(2n-1)
成立（证毕）．
点评：本题考查不等式的证明，着重考查分析法与放缩法的综合应用，考查分析与推理能力，属于难题．
练习册系列答案
相关题目
（2011•南通一模）设m，n为空间的两条直线，α，β为空间的两个平面，给出下列命题：
（1）若m∥α，m∥β，则α∥β；
（2）若m⊥α，m⊥β，则α∥β；
（3）若m∥α，n∥α，则m∥n；
（4）若m⊥α，n⊥α，则m∥n．
上述命题中，所有真命题的序号是
（2），（4）
（2），（4）
．
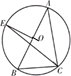（2011•南通一模） 选修4-1：几何证明选讲
锐角三角形ABC内接于⊙O，∠ABC=60°，∠BAC=40°．作OE⊥AB交劣弧
AB
于点E，连接EC，求∠OEC．
（2011•南通一模）选修4-2：矩阵与变换
曲线C1：x2+2y2=1在矩阵M=
12
01
的作用下变换为曲线C2，求C2的方程．
（2011•南通一模）选修4-4：坐标系与参数方程
P为曲线C1：
x=1+cosθ
y=sinθ
（θ为参数）上一点，求它到直线C2：
x=1+2t
y=2
（t为参数）距离的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网