题目内容
已知函数 ,数列an满足
,数列an满足 .
.(1)求数列{an}的通项公式;
(2)令Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1,求a2n-1-a2n+1及Tn;
(3)令
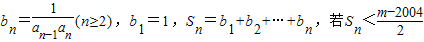 对一切n∈N*成立,求最小正整数m.
对一切n∈N*成立,求最小正整数m.
【答案】分析:本题考查的是数列与不等式的综合问题.在解答时:
(1)结合函数解析式和递推关系即可探索出数列的特点,再利用等差数列的特点即可求得数列{an}的通项公式;
(2)结合(1)的结论即可获得a2n-1-a2n+1的值,同时通过a2n-1•a2n-a2n•a2n+1的表达即可获得Tn中数列的通项,结合等差数列的知识即可获得问题的解答;
(3)首先利用(1)的结论对bn进行化简,再利用裂项的方法即可获得问题的解答.
解答:解:(1)由题意可知: ,
,
∴数列{an}为以1为首项,以 为公差的等差数列,
为公差的等差数列,
所以通向公式为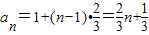 ,
,
即: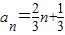 ,n∈N*;
,n∈N*;
(2)∵Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1,结合(1)的结论可知: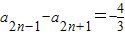
且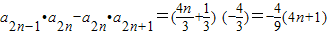 ,
,
∴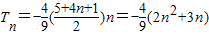 ,
,
故: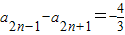 ,
,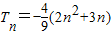 .
.
(3)∵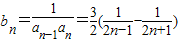
∴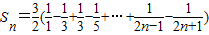
=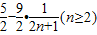
∴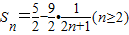
∴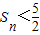
又因为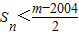 对一切n∈N*成立,
对一切n∈N*成立,
∴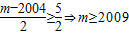
故:m的最小值为2009.
点评:本题考查的是数列与不等式的综合问题.在解答的过程当中充分体现了递推公式的知识、等差数列的知识、列项的方法以及恒成立问题的解答规律.值得同学们体会和反思.
(1)结合函数解析式和递推关系即可探索出数列的特点,再利用等差数列的特点即可求得数列{an}的通项公式;
(2)结合(1)的结论即可获得a2n-1-a2n+1的值,同时通过a2n-1•a2n-a2n•a2n+1的表达即可获得Tn中数列的通项,结合等差数列的知识即可获得问题的解答;
(3)首先利用(1)的结论对bn进行化简,再利用裂项的方法即可获得问题的解答.
解答:解:(1)由题意可知:
 ,
,∴数列{an}为以1为首项,以
 为公差的等差数列,
为公差的等差数列,所以通向公式为
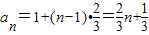 ,
,即:
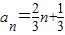 ,n∈N*;
,n∈N*;(2)∵Tn=a1a2-a2a3+a3a4-a4a5+…-a2na2n+1,结合(1)的结论可知:
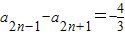
且
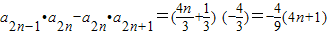 ,
,∴
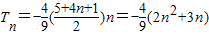 ,
,故:
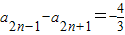 ,
,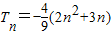 .
.(3)∵
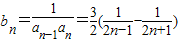
∴
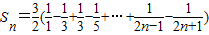
=
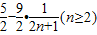
∴
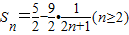
∴
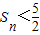
又因为
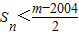 对一切n∈N*成立,
对一切n∈N*成立,∴
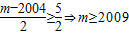
故:m的最小值为2009.
点评:本题考查的是数列与不等式的综合问题.在解答的过程当中充分体现了递推公式的知识、等差数列的知识、列项的方法以及恒成立问题的解答规律.值得同学们体会和反思.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 若数列{an}满a1=
若数列{an}满a1= ,an+1=f(an),n∈N*,则a2006+a2009+a2010= .
,an+1=f(an),n∈N*,则a2006+a2009+a2010= . 若数列{an}满a1=
若数列{an}满a1= ,an+1=f(an),n∈N*,则a2006+a2009+a2010= .
,an+1=f(an),n∈N*,则a2006+a2009+a2010= .