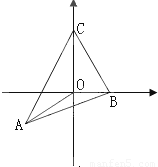
题目内容
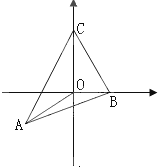 已知O为三角形ABC内一点,∠AOB=150°,∠BOC=90°,若
已知O为三角形ABC内一点,∠AOB=150°,∠BOC=90°,若| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
(1)用
| a |
| b |
| c |
(2)求
| a |
| b |
| c |
分析:(1)建立直角坐标系:可得
、
、
的坐标.设
=x
+y
,求得x和y的值,从而用
,
表示
.
(2)根据
•(
-
)=
•
-
•
,运算求得结果.
| a |
| b |
| c |
| c |
| a |
| b |
| a |
| b |
| c |
(2)根据
| a |
| b |
| c |
| a |
| b |
| a |
| c |
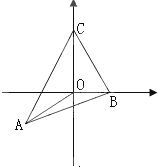
解答:解:(1)如图,建立直角坐标系:易知:
=(-
,-1),
=(1,0),
=(0,3).
设
=x
+y
,则(0,3)=x(-
,-1)+y(1,0)=(-
x+y,-x),
解得x=-3,y=-3
,即
=-3
-3
.
(2)
•(
-
)=
•
-
•
=(-
)-(-3)=3-
.
| a |
| 3 |
| b |
| c |
设
| c |
| a |
| b |
| 3 |
| 3 |
解得x=-3,y=-3
| 3 |
| c |
| a |
| 3 |
| b |
(2)
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| 3 |
| 3 |
点评:本题主要考查两个向量的数量积的运算,两个向量的坐标形式的运算,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
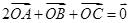 ,那么( )
,那么( )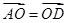 B、
B、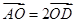 C、
C、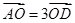 D、
D、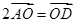
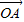 =
=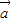 ,
,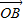 =
=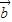 ,
,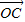 =
=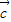 ,且|
,且|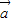 |=2,|
|=2,|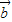 |=1,|
|=1,|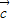 |=3,
|=3,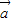 ,
,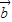 表示
表示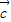
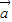 •(
•(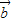 -
-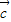 )
)