题目内容
已知函数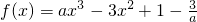 .
.
(1)讨论函数f(x)的单调性;
(2)若曲线y=f(x)上两点A,B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
(3)当x∈[-1,2]时,函数y=f(x)的图象上任意一点的切线斜率恒大于3a,求a的取值范围.
解:(1)由题设知a≠0,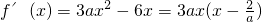 .
.
令f′(x)=0得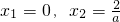 .
.
①当a>0时,若x∈(-∞,0),则f′(x)>0,则f(x)在区间(-∞,0)上是增函数;
若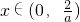 ,则f′(x)<0,则f(x)在区间
,则f′(x)<0,则f(x)在区间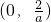 上是减函数;
上是减函数;
若 ,则f′(x)>0,则f(x)在间
,则f′(x)>0,则f(x)在间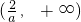 上是增函数.
上是增函数.
②当a<0时,若a≤-2,则a≥1,则f(x)在区间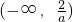 上是减函数;
上是减函数;
若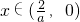 ,则f′(x)>0,则f(x)在区间
,则f′(x)>0,则f(x)在区间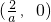 上是增函数;
上是增函数;
若x∈(0,+∞),则f′(x)<0,则f(x)在区间(0,+∞)上是减函数.
(2)由(1)的讨论及题设知,曲线y=f(x)上的两点A、B的纵坐标均为函数的极值.
且函数y=f(x)在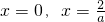 处分别取得极值
处分别取得极值 ,
,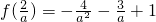 .
.
因为线段AB与x轴有公共点,所以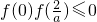 ,
,
即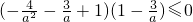 .所以
.所以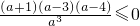 .
.
故a(a+1)(a-3)(a-4)≤0且a≠0.解得-1≤a<0或3≤a≤4
即所求实数a的取值范围是[-1,0)∪[3,4].
(3)可转化成f′(x)=3ax2-6x>3a在区间[-1,2]恒成立,
即3ax2-6x-3a>0在区间[-1,2]恒成立,
将x=-1和x=2代入使之成立,解得a>
∴a的取值范围( ,+∞)
,+∞)
分析:(1)先对函数f(x)进行求导,根据导函数大于0原函数单调递增,导函数小于0原函数单调递减进行讨论.
(2)由题意可值点AB应是函数f(x)的极值点,再根据线段AB与x轴有公共点可知以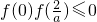 ,从而得到答案.
,从而得到答案.
(3)本小问可转化成f′(x)=3ax2-6x>3a在区间[-1,2]恒成立,即3ax2-6x-3a>0在区间[-1,2]恒成立,将x=-1和x=2代入使之成立,即可求出a的范围.
点评:本题主要考查函数的单调性、极值点与其导函数之间的关系.导数是高等数学下放到高中,是高考的热点问题,每年必考要给予重视.
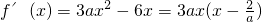 .
.令f′(x)=0得
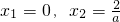 .
.①当a>0时,若x∈(-∞,0),则f′(x)>0,则f(x)在区间(-∞,0)上是增函数;
若
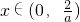 ,则f′(x)<0,则f(x)在区间
,则f′(x)<0,则f(x)在区间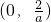 上是减函数;
上是减函数;若
 ,则f′(x)>0,则f(x)在间
,则f′(x)>0,则f(x)在间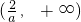 上是增函数.
上是增函数.②当a<0时,若a≤-2,则a≥1,则f(x)在区间
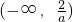 上是减函数;
上是减函数;若
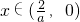 ,则f′(x)>0,则f(x)在区间
,则f′(x)>0,则f(x)在区间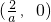 上是增函数;
上是增函数;若x∈(0,+∞),则f′(x)<0,则f(x)在区间(0,+∞)上是减函数.
(2)由(1)的讨论及题设知,曲线y=f(x)上的两点A、B的纵坐标均为函数的极值.
且函数y=f(x)在
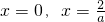 处分别取得极值
处分别取得极值 ,
,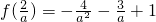 .
.因为线段AB与x轴有公共点,所以
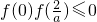 ,
,即
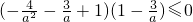 .所以
.所以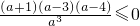 .
.故a(a+1)(a-3)(a-4)≤0且a≠0.解得-1≤a<0或3≤a≤4
即所求实数a的取值范围是[-1,0)∪[3,4].
(3)可转化成f′(x)=3ax2-6x>3a在区间[-1,2]恒成立,
即3ax2-6x-3a>0在区间[-1,2]恒成立,
将x=-1和x=2代入使之成立,解得a>

∴a的取值范围(
 ,+∞)
,+∞)分析:(1)先对函数f(x)进行求导,根据导函数大于0原函数单调递增,导函数小于0原函数单调递减进行讨论.
(2)由题意可值点AB应是函数f(x)的极值点,再根据线段AB与x轴有公共点可知以
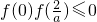 ,从而得到答案.
,从而得到答案.(3)本小问可转化成f′(x)=3ax2-6x>3a在区间[-1,2]恒成立,即3ax2-6x-3a>0在区间[-1,2]恒成立,将x=-1和x=2代入使之成立,即可求出a的范围.
点评:本题主要考查函数的单调性、极值点与其导函数之间的关系.导数是高等数学下放到高中,是高考的热点问题,每年必考要给予重视.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
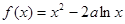 ,
,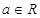
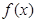 单调区间;
单调区间;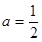 时,证明:当
时,证明:当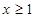 时,证明:
时,证明: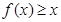 。
。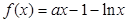
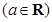 .
.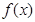 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对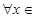
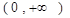 ,
,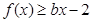 恒成立,求实数
恒成立,求实数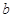 的取值范围.
的取值范围. 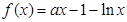
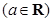 .
.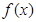 在定义域内的极值点的个数;
在定义域内的极值点的个数;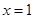 处取得极值,对
处取得极值,对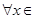
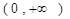 ,
,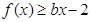 恒成立,求实数
恒成立,求实数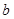 的取值范围;
的取值范围;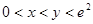 且
且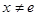 时,试比较
时,试比较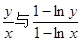 的大小.
的大小. .
. 函数
函数 的单调性;
的单调性; 为偶数时,正项数列
为偶数时,正项数列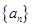 满足
满足 ,求
,求 时,求证:
时,求证: .
. 。(1)讨论函数
。(1)讨论函数 的单调性;(2)当
的单调性;(2)当 时,设
时,设 ,若
,若 时,
时, 恒成立。求整数
恒成立。求整数 的最大值。
的最大值。