题目内容
若点P在以F1,F2为焦点的椭圆上,PF2⊥F1F2,tan∠PF1F2=
,则椭圆的离心率为
.
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:在Rt△PF1F2中,F1F2=2c为焦距,利用正切的定义结合tan∠PF1F2=
,可得PF2=
c,再由勾股定理算出PF1=
c,根据椭圆的定义得2a=PF1+PF2=4c,最后根据离心率的计算公式,可以算出该椭圆的离心率.
| 3 |
| 4 |
| 3 |
| 2 |
| 5 |
| 2 |
解答:解:∵PF2⊥F1F2,tan∠PF1F2=
,
∴
=
,结合F1F2=2c为焦距,可得PF2=
c
因此,根据勾股定理可得PF1=
=
c
∴根据椭圆的定义,得椭圆的长轴2a=PF1+PF2=
c+
c=4c
由此可得椭圆的离心率为e=
=
=
=
故答案为:
| 3 |
| 4 |
∴
| PF2 |
| F1F2 |
| 3 |
| 4 |
| 3 |
| 2 |
因此,根据勾股定理可得PF1=
| PF22+F1F12 |
| 5 |
| 2 |
∴根据椭圆的定义,得椭圆的长轴2a=PF1+PF2=
| 3 |
| 2 |
| 5 |
| 2 |
由此可得椭圆的离心率为e=
| c |
| a |
| 2c |
| 2a |
| 2c |
| 4c |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题根据椭圆的焦距与椭圆上一点构成直角三角形,在已知一个角正切的基础之上求椭圆的离心率,着重考查了直角三角形的性质和椭圆的基本概念,属于基础题.

练习册系列答案
相关题目
 ,则椭圆的离心率为___________
,则椭圆的离心率为___________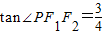 ,则椭圆的离心率为 .
,则椭圆的离心率为 .