题目内容
(16分)如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的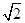 倍,
倍,
P为侧棱SD上的点。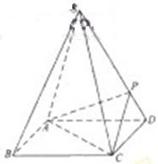
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 使得BE∥平
面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
【答案】
略
【解析】解法一:
(Ⅰ)连BD,设AC交BD于O,由题意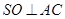 。在正方形ABCD中,
。在正方形ABCD中,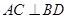 ,所以
,所以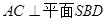 ,得
,得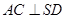 .[来源:学.科.网Z.X.X.K]
.[来源:学.科.网Z.X.X.K]
(Ⅱ)设正方形边长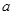 ,则
,则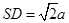 。
。
又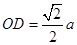 ,所以
,所以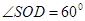 ,
,
连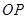 ,由(Ⅰ)知
,由(Ⅰ)知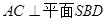 ,所以
,所以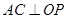 ,
,
且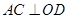 ,所以
,所以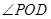 是二面角
是二面角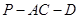 的平面角。
的平面角。
由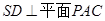 ,知
,知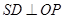 ,所以
,所以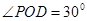 ,
,
即二面角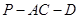 的大小为
的大小为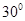 。
。
(Ⅲ)在棱SC上存在一点E,使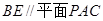
由(Ⅱ)可得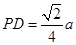 ,故可在
,故可在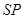 上取一点
上取一点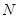 ,使
,使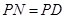 ,过
,过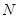 作
作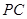 的平行线与
的平行线与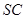 的交点即为
的交点即为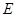 。连BN。在
。连BN。在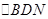 中知
中知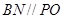 ,又由于
,又由于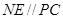 ,故平面
,故平面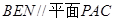 ,得
,得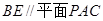 ,由于
,由于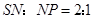 ,故
,故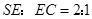 .
.
解法二:
(Ⅰ);连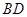 ,设
,设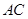 交于
交于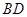 于
于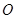 ,由题意知
,由题意知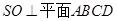 .以O为坐标原点,
.以O为坐标原点,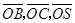 分别为
分别为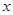 轴、
轴、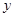 轴、
轴、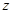 轴正方向,建立坐标系
轴正方向,建立坐标系 如图。[来源:ZXXK]
如图。[来源:ZXXK]
设底面边长为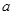 ,则高
,则高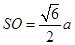 。
。
于是 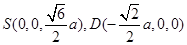
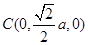
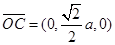
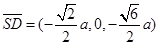
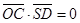
故
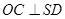
从而 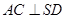
(Ⅱ)由题设知,平面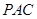 的一个法向量
的一个法向量 ,平面
,平面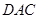 的一个法向量
的一个法向量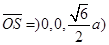 ,设所求二面角为
,设所求二面角为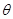 ,则
,则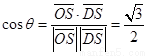 ,所求二面角的大小为
,所求二面角的大小为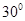 [来源:Z_xx_k.Com]
[来源:Z_xx_k.Com]
(Ⅲ)在棱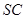 上存在一点
上存在一点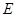 使
使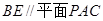 .[来源:]
.[来源:]
由(Ⅱ)知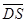 是平面
是平面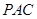 的一个法向量,
的一个法向量,
且 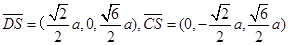
设 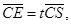
则 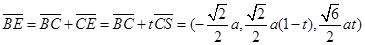 [来源:ZXXK]
[来源:ZXXK]
而 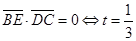
即当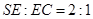 时,
时,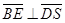 [来源:ZXXK]
[来源:ZXXK]
而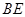 不在平面
不在平面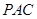 内,故
内,故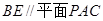

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.