题目内容
设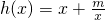 ,
,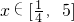 ,其中m是不等于零的常数,
,其中m是不等于零的常数,
(1)(理)写出h(4x)的定义域;
(文)m=1时,直接写出h(x)的值域;
(2)(文、理)求h(x)的单调递增区间;
(3)已知函数f(x)(x∈[a,b]),定义:f1(x)=minf(t)|a≤t≤x(x∈[a,b]),f2(x)=maxf(t)|a≤t≤x(x∈[a,b]).其中,minf(x)|x∈D表示函数f(x)在D上的最小值,maxf(x)|x∈D表示函数f(x)在D上的最大值.例如:f(x)=cosx,x∈[0,π],则f1(x)=cosx,x∈[0,π],f2(x)=1,x∈[0,π].
(理)当m=1时,设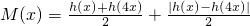 ,不等式t≤M1(x)-M2(x)≤n恒成立,求t,n的取值范围;
,不等式t≤M1(x)-M2(x)≤n恒成立,求t,n的取值范围;
(文)当m=1时,|h1(x)-h2(x)|≤n恒成立,求n的取值范围.
解:理(1)∵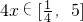 ,
,
∴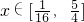
∴h(4x)的定义域为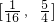
(2)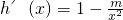
m<0时,h(x)在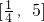 递增;
递增;
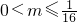 时,h(x)在
时,h(x)在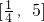 递增
递增
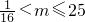 时,h(x)在
时,h(x)在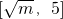 递增
递增
(3)由题知: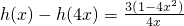
所以,h(x)>h(4x)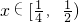
h(x)=h(4x)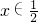
h(x)<h(4x)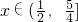
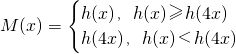
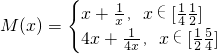
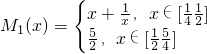
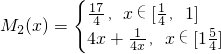
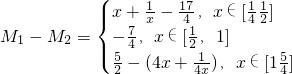
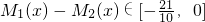
∴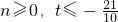
文:(1)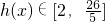
(2)m<0时,h(x)在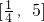 递增
递增
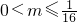 时,h(x)在
时,h(x)在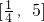 递增
递增
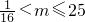 时,h(x)在
时,h(x)在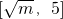 递增
递增
(3)
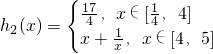
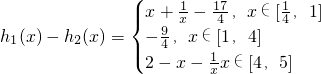
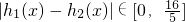
所以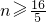
分析:(1)令4x在h(x)的定义域内,求出x的范围,写出区间形式即为h(4x)的定义域.
(2)对m分类讨论,利用导函数的符号,当导函数大于0时对应的区间为递增区间;导函数小于0时,对应的区间为递减区间;求出函数的单调区间.
(3)通过解不等式,比较出h(x)与h(4x)的大小,求出m(x)的解析式;求出M1(x),M2(x)求出M1(x)-M2(x)的值域,求出t,n的范围.
点评:本题考查抽象函数的定义域的求法:知f(x)的定义域为[a,b],求f(mx+n)的定义域只要解不等式a≤mx+n≤b即可、考查研究函数的单调区间时,若含参数一般需要讨论.分段函数的处理方法是先分再合的策略.
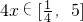 ,
,∴
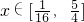
∴h(4x)的定义域为
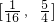
(2)
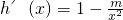
m<0时,h(x)在
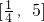 递增;
递增;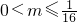 时,h(x)在
时,h(x)在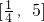 递增
递增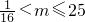 时,h(x)在
时,h(x)在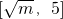 递增
递增(3)由题知:
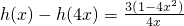
所以,h(x)>h(4x)
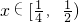
h(x)=h(4x)
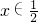
h(x)<h(4x)
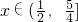
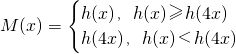
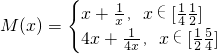
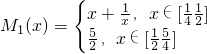
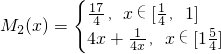
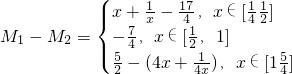
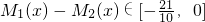
∴
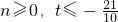
文:(1)
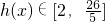
(2)m<0时,h(x)在
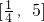 递增
递增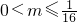 时,h(x)在
时,h(x)在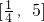 递增
递增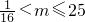 时,h(x)在
时,h(x)在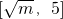 递增
递增(3)

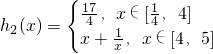
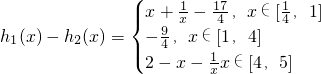
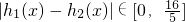
所以
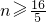
分析:(1)令4x在h(x)的定义域内,求出x的范围,写出区间形式即为h(4x)的定义域.
(2)对m分类讨论,利用导函数的符号,当导函数大于0时对应的区间为递增区间;导函数小于0时,对应的区间为递减区间;求出函数的单调区间.
(3)通过解不等式,比较出h(x)与h(4x)的大小,求出m(x)的解析式;求出M1(x),M2(x)求出M1(x)-M2(x)的值域,求出t,n的范围.
点评:本题考查抽象函数的定义域的求法:知f(x)的定义域为[a,b],求f(mx+n)的定义域只要解不等式a≤mx+n≤b即可、考查研究函数的单调区间时,若含参数一般需要讨论.分段函数的处理方法是先分再合的策略.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
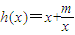 ,
,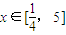 ,其中m是不等于零的常数,
,其中m是不等于零的常数,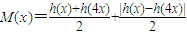 ,不等式t≤M1(x)-M2(x)≤n恒成立,求t,n的取值范围;
,不等式t≤M1(x)-M2(x)≤n恒成立,求t,n的取值范围;