题目内容
已知函数 R),g(x)=lnx.
R),g(x)=lnx.(1)求函数F(x)=f(x)+g(x)的单调区间;
(2)若关于x的方程
 (e为自然对数的底数)只有一个实数根,求a的值.
(e为自然对数的底数)只有一个实数根,求a的值.
【答案】分析:(1)先求出求函数F(x)=f(x)+g(x)的导函数,分情况求出导数为0的根进而求出函数的单调区间(注意是在定义域内求单调区间);
(2)先把问题转化为 只有一个实数根;再利用导函数分别求出等号两端的极值,在下面画出草图,结合草图即可求出结论.
只有一个实数根;再利用导函数分别求出等号两端的极值,在下面画出草图,结合草图即可求出结论.
解答:(1)解:函数 的定义域为(0,+∞).
的定义域为(0,+∞).
∴ =
= .
.
①当△=1+4a≤0,即 时,得x2+x-a≥0,则F′(x)≥0.
时,得x2+x-a≥0,则F′(x)≥0.
∴函数F(x)在(0,+∞)上单调递增.(2分)
②当△=1+4a>0,即 时,令F′(x)=0,得x2+x-a=0,
时,令F′(x)=0,得x2+x-a=0,
解得 .
.
(ⅰ)若 ,则
,则 .
.
∵x∈(0,+∞),∴F′(x)>0,
∴函数F(x)在(0,+∞)上单调递增.(4分)
(ⅱ)若a>0,则 时,F′(x)<0;
时,F′(x)<0; 时,F′(x)>0,
时,F′(x)>0,
∴函数F(x)在区间 上单调递减,在区间
上单调递减,在区间 上单调递增.
上单调递增.
综上所述,当a≤0时,函数F(x)的单调递增区间为(0,+∞);
当a>0时,函数F(x)的单调递减区间为 ,
,
单调递增区间为 .(8分)
.(8分)
(2)解:由 ,得
,得 ,化为
,化为 .
.
令 ,则
,则 .
.
令h′(x)=0,得x=e.
当0<x<e时,h′(x)>0;当x>e时,h′(x)<0.
∴函数h(x)在区间(0,e)上单调递增,在区间(e,+∞)上单调递减.
∴当x=e时,函数h(x)取得最大值,其值为 .(10分)
.(10分)
而函数m(x)=x2-2ex+a=(x-e)2+a-e2,
当x=e时,函数m(x)取得最小值,其值为m(e)=a-e2.(12分)
∴当 ,即
,即 时,方程
时,方程 只有一个根.(14分)
只有一个根.(14分)
点评:本题第一问考查利用导数研究函数的单调性.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数这一章最基本的知识,也是.教学中的重点和难点,学生应熟练掌握.
(2)先把问题转化为
 只有一个实数根;再利用导函数分别求出等号两端的极值,在下面画出草图,结合草图即可求出结论.
只有一个实数根;再利用导函数分别求出等号两端的极值,在下面画出草图,结合草图即可求出结论.解答:(1)解:函数
 的定义域为(0,+∞).
的定义域为(0,+∞).∴
 =
= .
.①当△=1+4a≤0,即
 时,得x2+x-a≥0,则F′(x)≥0.
时,得x2+x-a≥0,则F′(x)≥0.∴函数F(x)在(0,+∞)上单调递增.(2分)
②当△=1+4a>0,即
 时,令F′(x)=0,得x2+x-a=0,
时,令F′(x)=0,得x2+x-a=0,解得
 .
.(ⅰ)若
 ,则
,则 .
.∵x∈(0,+∞),∴F′(x)>0,
∴函数F(x)在(0,+∞)上单调递增.(4分)
(ⅱ)若a>0,则
 时,F′(x)<0;
时,F′(x)<0; 时,F′(x)>0,
时,F′(x)>0,∴函数F(x)在区间
 上单调递减,在区间
上单调递减,在区间 上单调递增.
上单调递增.综上所述,当a≤0时,函数F(x)的单调递增区间为(0,+∞);
当a>0时,函数F(x)的单调递减区间为
 ,
,单调递增区间为
 .(8分)
.(8分)(2)解:由
 ,得
,得 ,化为
,化为 .
.令
 ,则
,则 .
.令h′(x)=0,得x=e.
当0<x<e时,h′(x)>0;当x>e时,h′(x)<0.
∴函数h(x)在区间(0,e)上单调递增,在区间(e,+∞)上单调递减.
∴当x=e时,函数h(x)取得最大值,其值为
 .(10分)
.(10分)而函数m(x)=x2-2ex+a=(x-e)2+a-e2,
当x=e时,函数m(x)取得最小值,其值为m(e)=a-e2.(12分)
∴当
 ,即
,即 时,方程
时,方程 只有一个根.(14分)
只有一个根.(14分)点评:本题第一问考查利用导数研究函数的单调性.利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数这一章最基本的知识,也是.教学中的重点和难点,学生应熟练掌握.

练习册系列答案
相关题目
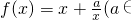 R),g(x)=lnx.
R),g(x)=lnx.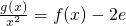 (e为自然对数的底数)只有一个实数根,求a的值.
(e为自然对数的底数)只有一个实数根,求a的值. R),g(x)=lnx
R),g(x)=lnx (e为自然对数的底数)只有一个实数根,求a的值.
(e为自然对数的底数)只有一个实数根,求a的值. R),g(x)=lnx.
R),g(x)=lnx. (e为自然对数的底数)只有一个实数根,求a的值.
(e为自然对数的底数)只有一个实数根,求a的值. R),g(x)=lnx.
R),g(x)=lnx. (e为自然对数的底数)只有一个实数根,求a的值.
(e为自然对数的底数)只有一个实数根,求a的值.