题目内容

13、若函数y=（sinx-a）2+1在sinx=1时取得最大值，在sinx=a时取得最小值，则实数a的取值范围为
-1≤a≤0
．
分析：根据-1≤sinx≤1，确定a的范围，根据sinx=1时取得最大值，确定（-1-a）2+1≤（1-a）2+1，从而求出a的范围．
解答：解：sinx=a时取最小值
因为-1≤sinx≤1
所以-1≤a≤1
因为sinx=1时取最大值，所以当sinx=-1时y的值不比sinx=1时y的值大
（-1-a）2+1≤（1-a）2+1
1+2a+a2+1=1-2a+a2+1
a≤0
综合得：-1≤a≤0
故答案为：-1≤a≤0
点评：本题考查三角函数的最值，注意三角函数y=sinx的有界性，才能正确处理a的取值，避免错误解题，本题考查计算能力，分析问题解决问题的能力．
练习册系列答案
相关题目
已知二次函数，f（x）=x2+ax（a∈R）．
（1）若函数y=f(sinx+
3
cosx)(x∈R)的最大值为
16
3
，求f（x）的最小值；
（2）当a=2时，设n∈N*，S=
n
f(n)
+
n+1
f(n+1)
+…+
3n-1
f(3n-1)
+
3n
f(3n)
，求证：
3
4
＜S＜2；
（3）当a＞2时，求证f（sin2xlog2sin2x+cos2xlog2cos2x）≧1-a，其中x∈R，x≠kπ且x≠kπ+
π
2
（k∈z）
已知二次函数f（x）=x2+ax（a∈R）
（1）若函数y=f(sinx+
3
cosx)(x∈R)的最大值为
16
3
，求f(x)的最小值；
（2）当a=2是，设n∈N*，S=
n
f(n)
+
n+1
f(n+1)
+…+
3n-1
f(3n-1)
+
3n
f(3n)
，求证：
3
4
＜S＜2．

已知二次函数f(x)=x2+ax（）．

（1）若函数y=f(sinx+cosx)(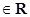)的最大值为，求f(x)的最小值；

（2）当a>2时,求证：f(sin2xlog2sin2x+cos2xlog2cos2x)1–a.其中x∈R,x¹kp且x¹kp(k∈Z).

 
若函数y=（sinx-a）2+1在sinx=1时取得最大值，在sinx=a时取得最小值，则实数a的取值范围为 ______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网