题目内容
把一个半径为r的实心铁球O熔化铸成两个实心小球O1与O2，假设没有任何损耗、设铁球O的表面积为S，小球O1的半径为r1，表面积为S1，小球O2的半径为r2，两个小球的半径之比r1：r2=1：2，那么球O1的表面积与球O的表面积之比S1：S=（ ）
分析：两个球的表面积之比就是半径之比的平方，求出半径之间的关系，即可得到结论．
解答：解：由题意，设两个小球的半径分别为x，2x，则
π(x3+8x3)=
πr3
∴r=
x
∴球O1的表面积与球O的表面积之比S1：S=x2：(
x)2=1：3
故选B．
| 4 |
| 3 |
| 4 |
| 3 |
∴r=
| 3 | 9 |
∴球O1的表面积与球O的表面积之比S1：S=x2：(
| 3 | 9 |
| 3 | 3 |
故选B．
点评：本题是基础题，考查相似比的知识，面积之比是相似比的平方，确定半径之间的关系是关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
，那么球O1的表面积与球O的表面积之比
= .
，那么球O1的表面积与球O的表面积之比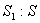
=
.