题目内容
(本题12分)现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ,命中得
,命中得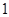 分,没有命中得
分,没有命中得 分;向乙靶射击两次,每次命中的概率为
分;向乙靶射击两次,每次命中的概率为 ,每命中一次得
,每命中一次得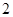 分,没有命中得
分,没有命中得 分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(1)求该射手恰好命中一次的概率;(2)求该射手的总得分
分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.(1)求该射手恰好命中一次的概率;(2)求该射手的总得分 的分布列及数学期望
的分布列及数学期望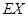 .
.
(1)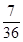 ;(2)分布列见解析,数学期望
;(2)分布列见解析,数学期望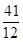 。
。
解析试题分析:(1)记“该射手恰好命中一次”为事件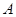 ,“该射手射击甲靶命中”为事件
,“该射手射击甲靶命中”为事件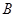 ,“该射手第一次射击乙靶命中”为事件
,“该射手第一次射击乙靶命中”为事件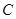 ,“该射手第二次射击乙靶命中”为事件
,“该射手第二次射击乙靶命中”为事件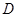 .由题意知
.由题意知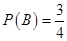 ,
,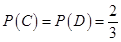 .
.
由于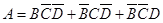 ,
,
所以 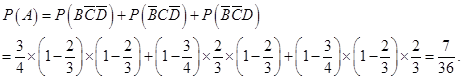 6分
6分
(Ⅱ)根据题意, 的所有可能取值为
的所有可能取值为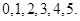 7分
7分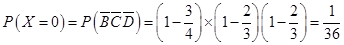 ,
,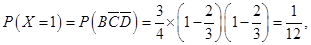
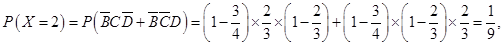
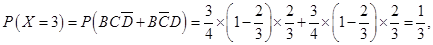
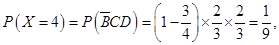
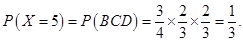 10分
10分
所以 的分布列为
的分布列为

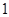
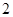

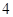
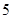
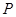
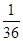
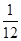
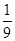
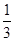
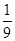
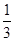
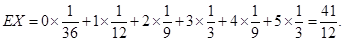 12分
12分
考点:离散型随机变量的期望与方差;互斥事件的概率加法公式;相互独立事件的概率乘法公式;随机变量的分布列和数学期望。
点评:本题主要考查了离散型随机变量的期望,以及分布列和事件的对立性和互斥性,同时考查了计算能力和分析问题的能力,属于中档题。在计算分布列时,要注意考虑周全,不要遗漏情况。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
(1)求z的值;
(2)用分层抽样的方法在A样式灯泡中抽取一个容量为5的样本,从这个样本中任取2个灯泡,求至少有1个10W的概率.
(本小题共12分)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| | “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(Ⅱ)试估计生活垃圾投放错误的概率;
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为
 ,其中
,其中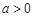 ,
,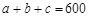 。当数据
。当数据 的方差
的方差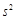 最大时,写出
最大时,写出 的值(结论不要求证明),并求此时
的值(结论不要求证明),并求此时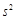 的值.
的值.(注:
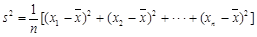 ,其中
,其中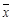 为数据
为数据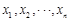 的平均数)
的平均数)  和
和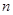 ,将
,将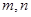 作为Q点的横、纵坐标,
作为Q点的横、纵坐标,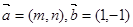 的夹角为
的夹角为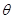 ,求
,求 的概率;
的概率;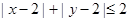 内的概率.
内的概率.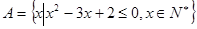 ,集合
,集合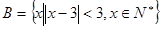 ,
,
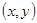 所有可能的结果;
所有可能的结果;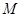 中任取一个元素,求“
中任取一个元素,求“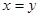 ”的概率
”的概率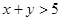 ”的概率.
”的概率.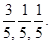
 与
与 ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为 。
。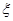 ,求
,求