题目内容
(本小题12分)已知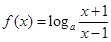 (
(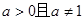 ).
).
(1)判断函数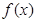 的奇偶性,并证明;
的奇偶性,并证明;
(2)若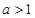 ,用单调性定义证明函数
,用单调性定义证明函数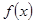 在区间
在区间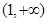 上单调递减;
上单调递减;
(3)是否存在实数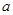 ,使得
,使得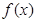 的定义域为
的定义域为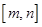 时,值域为
时,值域为
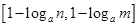 ,若存在,求出实数
,若存在,求出实数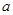 的取值范围;若不存在,则说明理由.
的取值范围;若不存在,则说明理由.
【答案】
(1)奇函数.(2)函数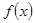 在区间
在区间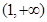 上单调递减.
上单调递减.
(3)满足题目条件的实数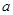 存在,实数
存在,实数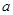 的取值范围是
的取值范围是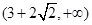 .
.
【解析】
试题分析:(1)根据对数函数的真数大于0建立不等式,解之即可求出函数的定义域,判定是否对称,然后根据函数奇偶性的定义进行判定即可;
(2)任取x1,x2∈(1,+∞),且x1<x2,然后比较真数的大小,从而得到f(x1)与f(x2)的大小,最后根据单调性的定义进行判定即可;
(3)假设存在实数a满足题目条件,然后根据函数在区间[m,n]上单调性建立等式关系,然后转化成方程x2+(1-a)x+a=0在区间(1,+∞)上有两个不同的实根,从而可求出a的取值范围.
解:(1)由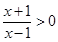 得:
得: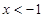 或
或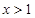 .
.
所以,函数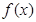 的定义域为
的定义域为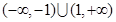 .
.
又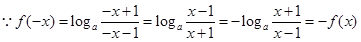
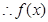 为奇函数.
为奇函数.
(2)任取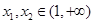 ,且
,且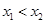 ,则
,则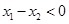 .
.
因为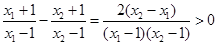
所以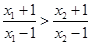 ,又因为
,又因为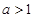 ,所以
,所以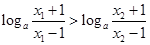 ,
,
故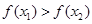 ,所以,函数
,所以,函数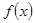 在区间
在区间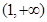 上单调递减.
上单调递减.
(3)假设存在实数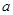 满足题目条件.
满足题目条件.
由题意得: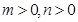 ,又
,又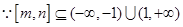 ,
,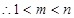
又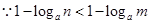 ,
, ,
,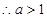 .
.
故,由(2)得:函数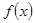 在区间
在区间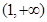 上单减.所以,函数
上单减.所以,函数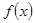 在区间
在区间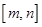 上单调递减.
上单调递减.
故,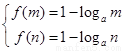 ,所以
,所以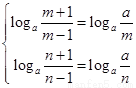 ,
,
所以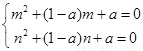 ,
,
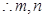 是方程
是方程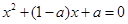 的两个不同的实根.
的两个不同的实根.
故,方程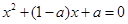 在区间
在区间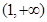 上有两个不同的实根.
上有两个不同的实根.
则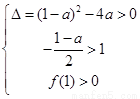 ,解得:
,解得: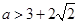 .又
.又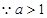 ,
,
所以,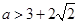 所以,满足题目条件的实数
所以,满足题目条件的实数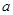 存在,实数
存在,实数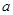 的取值范围是
的取值范围是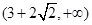 .
.
考点:本题主要考查了函数奇偶性的判定,以及单调性的判定和奇偶性与单调性的综合应用,同时考查了转化的思想,属于中档题.
点评:解决该试题的关键是对于方程在某个区间上方有几个不同的实数根的问题,常常转化为分析参数来求解其范围。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线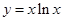
 处的切线方程。
处的切线方程。