题目内容
已知菱形ABCD与矩形BDEF所在平面互相垂直，且BD=2BF，若M为EF的中点，求证：BM∥平面AEC．
证明：连接EO，
∵EM平行且等于BO
∴四边形EOBM为平行四边形
∴EO∥BM
又∵EO?平面AEC，BM?平面AEC
∴BM∥平面AEC
分析：欲证BM∥平面AEC，根据直线与平面平行的判定定理可知只需证BM与平面AEC内一直线平行，连接EO，EO∥BM，EO?平面AEC，BM?平面AEC，满足定理条件．
点评：本题考查线面平行的推导．在证明线面平行时，其常用方法是在平面内找已知直线平行的直线．当然也可以用面面平行来推导线面平行．
∵EM平行且等于BO
∴四边形EOBM为平行四边形
∴EO∥BM
又∵EO?平面AEC，BM?平面AEC
∴BM∥平面AEC
分析：欲证BM∥平面AEC，根据直线与平面平行的判定定理可知只需证BM与平面AEC内一直线平行，连接EO，EO∥BM，EO?平面AEC，BM?平面AEC，满足定理条件．
点评：本题考查线面平行的推导．在证明线面平行时，其常用方法是在平面内找已知直线平行的直线．当然也可以用面面平行来推导线面平行．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
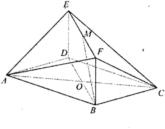已知菱形ABCD与矩形BDEF所在平面互相垂直，且BD=2BF，若M为EF的中点，BD∩AC=O