题目内容
3.在△ABC中,a,b,c分别为角A,B,C的对边,4sin2$\frac{B+C}{2}$-cos2A=$\frac{7}{2}$.(1)求A的度数;
(2)若$\overrightarrow{AB}•\overrightarrow{CA}$=-12,求△ABC的面积;
(3)若b+c=1,求三角形周长的取值范围.
分析 (1)先根据二倍角的余弦函数公式及诱导公式化简得到关于cosA的一元二次方程,解出cosA,根据角的范围,利用特殊角的三角函数值求出A即可;
(2)利用向量的数量积求出bc=24,利用三角形的面积公式进行求解即可.
(3)根据余弦定理结合基本不等式求出a的取值范围即可求出周长的取值范围.
解答 解:(1)由4sin2$\frac{B+C}{2}$-cos2A=$\frac{7}{2}$得:2[1-cos(B+C)]-cos2A=$\frac{7}{2}$,
即4cos2A-4cosA+1=0,
则(2cosA-1)2=0,
解得cosA=$\frac{1}{2}$,
∴A=$\frac{π}{3}$.
(2)∵$\overrightarrow{AB}•\overrightarrow{CA}$=-12,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=12,
即$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cosA=$\frac{1}{2}$bc=12,
∴bc=24,
∴△ABC的面积S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×24×\frac{\sqrt{3}}{2}$=6$\sqrt{3}$.
(3)∵b+c=1,
∴1=b+c$≥2\sqrt{bc}$,
即0<bc$≤\frac{1}{4}$,当且仅当b=c=$\frac{1}{2}$取等号,
则由余弦定理得a2=b2+c2-2bccos$\frac{π}{3}$=b2+c2-bc=(b+c)2-3bc=1-3bc,
∵0<bc$≤\frac{1}{4}$,∴-$\frac{1}{4}$≤-bc<0,
∴-$\frac{3}{4}$≤-3bc<0,$\frac{1}{4}$≤1-3bc<1,
即$\frac{1}{4}$≤a2<1,则$\frac{1}{2}$≤a<1,
则$\frac{1}{2}$+1≤a+b+c<1+1,
即$\frac{3}{2}$≤a+b+c<2,
即三角形的周长的取值范围是[$\frac{3}{2}$,2).
点评 本题主要考查三角函数式的化简,以及三角形面积公式的应用,结合余弦定理以及基本不等式是解决本题的关键.综合性较强,涉及的知识点较多.

| A. | ${(\frac{1}{4})^2}×(\frac{3}{4})$ | B. | ${(\frac{3}{4})^2}×(\frac{1}{4})$ | C. | $C_3^2{(\frac{1}{4})^2}×(\frac{3}{4})$ | D. | $C_3^2{(\frac{3}{4})^2}×(\frac{1}{4})$ |
 如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1E夹角的余弦值为( )
如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1E夹角的余弦值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{5}{2}$ |
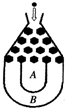 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,则小球落入A袋中的概率为$\frac{3}{4}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,则小球落入A袋中的概率为$\frac{3}{4}$.