题目内容
在直角坐标平面内,以坐标原点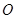 为极点、
为极点、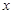 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点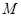 的极坐标为
的极坐标为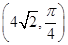 ,曲线
,曲线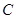 的参数方程为
的参数方程为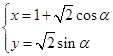 (
( 为参数),则点
为参数),则点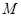 到曲线
到曲线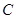 上的点的距离的最小值为 .
上的点的距离的最小值为 .
 为极点、
为极点、 轴的非负半轴为极轴建立极坐标系,已知点
轴的非负半轴为极轴建立极坐标系,已知点 的极坐标为
的极坐标为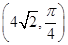 ,曲线
,曲线 的参数方程为
的参数方程为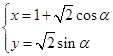 (
(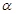 为参数),则点
为参数),则点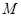 到曲线
到曲线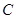 上的点的距离的最小值为 .
上的点的距离的最小值为 .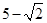
试题分析:由已知得,点
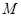 的直角坐标为
的直角坐标为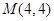 ,曲线
,曲线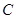 的普通方程为
的普通方程为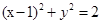 ,表示以
,表示以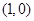 为圆心,
为圆心,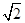 为半径的圆,故点
为半径的圆,故点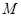 到曲线
到曲线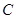 上的点的距离的最小值为
上的点的距离的最小值为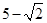 .
.
练习册系列答案
相关题目
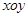 中,曲线
中,曲线 的参数方程为
的参数方程为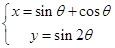 (
( 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点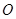 为极点,
为极点,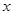 轴的正半轴为极轴建立极坐标,曲线
轴的正半轴为极轴建立极坐标,曲线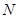 的极坐标方程为
的极坐标方程为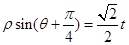 (其中
(其中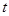 为常数).
为常数).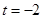 时,求曲线
时,求曲线 (
( 为参数)的倾斜角是
为参数)的倾斜角是 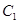 :
: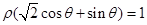 与曲线
与曲线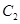 :
: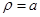
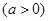 的一个交点在极轴上,则
的一个交点在极轴上,则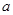 =_______.
=_______.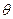 为参数,则圆
为参数,则圆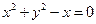 的参数方程为 .
的参数方程为 .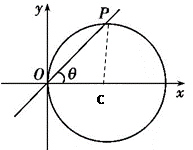
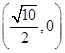 作倾斜角为α的直线与曲线x2+2y2=1交于点M、N,求|PM|·|PN|的最小值及相应的α的值.
作倾斜角为α的直线与曲线x2+2y2=1交于点M、N,求|PM|·|PN|的最小值及相应的α的值.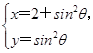 (θ为参数)化为普通方程.
(θ为参数)化为普通方程.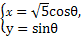 (0≤θ<π)和
(0≤θ<π)和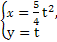 (t∈R),求它们的交点坐标.
(t∈R),求它们的交点坐标.