题目内容
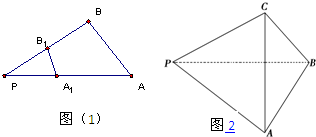 在△PAB中A1∈PA,B1∈PB,如图(1)所示,则△PA1B1和△PAB具有面积关系
在△PAB中A1∈PA,B1∈PB,如图(1)所示,则△PA1B1和△PAB具有面积关系| S△PA1B1 |
| S△PAB |
| PA 1•PB 1 |
| PA •PB |
分析:根据类比推理确定空间中类似的结论.
解答:解:结论:在三棱锥P-ABC中,A1∈PA,B1∈PB,C1∈PC,则两三棱锥P-A1B1C1和P-ABC体积具有关系式:
=
.…
如图(2)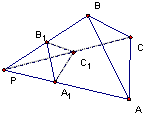
证明:过B1作B1H1⊥面PAC于H1,过B作BH⊥面PAC于H,则B1H1∥BH,
则点B,B1,P,H1,H共面,易证:点P,H1,H三点共线.
因为△B1PH1∽△BPH,所以
=
由平面几何可知:
=
,
=
=
=
| VP-A1B1C1 |
| VP-ABC |
| PA1•PB1•PC1 |
| PA•PB•PC |
如图(2)

证明:过B1作B1H1⊥面PAC于H1,过B作BH⊥面PAC于H,则B1H1∥BH,
则点B,B1,P,H1,H共面,易证:点P,H1,H三点共线.
因为△B1PH1∽△BPH,所以
| B1H1 |
| BH |
| PB1 |
| PB |
由平面几何可知:
| S△PA1C1 |
| S△PAC |
| PA1?PC1 |
| PA?PC |
| VP-A1B1C1 |
| VP-ABC |
| VB1-PA1C1 |
| VB-PAC |
| ||
|
| PA1?PB1?PC1 |
| PA?PB?PC |
点评:本题主要考查类比推理的应用,要求根据平面之间的关系类比到空间中,考查学生的推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
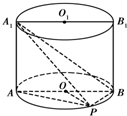 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.