题目内容
如图,在棱长为2的正方体ABCD-A1B1C1D1中,以底面正方形ABCD的中心为坐标原点O,分别以射线OB,OC,AA1的指向为x轴、y轴、z轴的正方向,建立空间直角坐标系.试写出正方体八个顶点的坐标.
【答案】分析:由题意直接求解OB,OC,然后写出正方体八个顶点的坐标.
解答:解 设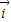 ,
,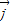 ,
,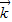 分别是与x轴、y轴、z轴的正方向方向相同的单位坐标向量.因为底面正方形的中心为O,边长为2,所以OB=
分别是与x轴、y轴、z轴的正方向方向相同的单位坐标向量.因为底面正方形的中心为O,边长为2,所以OB=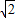 .由于点B在x轴的正半轴上,所以
.由于点B在x轴的正半轴上,所以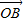 =
=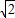
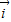 ,即点B的坐标为(
,即点B的坐标为(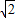 ,0,0).同理可得C(0,
,0,0).同理可得C(0,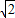 ,0),D(-
,0),D(-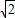 ,0,0),A(0,-
,0,0),A(0,-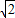 ,0).
,0).
又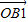 =
=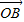 +
+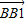 =
=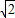
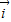 +2
+2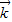 ,所以
,所以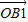 =(
=(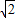 ,0,2).即点B1的坐标为(
,0,2).即点B1的坐标为(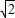 ,0,2).
,0,2).
同理可得C1(0,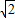 ,2),D1(-
,2),D1(-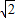 ,0,2),A1(0,-
,0,2),A1(0,-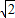 ,2).
,2).
点评:本题考查空间中点的终边的求法,基本知识的应用.
解答:解 设
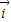 ,
,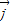 ,
,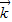 分别是与x轴、y轴、z轴的正方向方向相同的单位坐标向量.因为底面正方形的中心为O,边长为2,所以OB=
分别是与x轴、y轴、z轴的正方向方向相同的单位坐标向量.因为底面正方形的中心为O,边长为2,所以OB=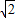 .由于点B在x轴的正半轴上,所以
.由于点B在x轴的正半轴上,所以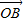 =
=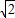
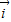 ,即点B的坐标为(
,即点B的坐标为(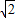 ,0,0).同理可得C(0,
,0,0).同理可得C(0,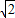 ,0),D(-
,0),D(-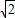 ,0,0),A(0,-
,0,0),A(0,-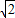 ,0).
,0).又
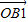 =
=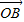 +
+ =
=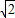
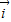 +2
+2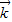 ,所以
,所以 =(
=(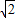 ,0,2).即点B1的坐标为(
,0,2).即点B1的坐标为(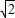 ,0,2).
,0,2).同理可得C1(0,
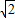 ,2),D1(-
,2),D1(-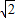 ,0,2),A1(0,-
,0,2),A1(0,-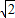 ,2).
,2).点评:本题考查空间中点的终边的求法,基本知识的应用.

练习册系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )






