题目内容
在△ABC中,2sinAsinBcosC=sinAsinCcosB+sinBsinCcosA,则内角C
- A.最大为60°
- B.最小为60°
- C.最大为90°
- D.最小为90°
A
分析:根据正弦、余弦定理化简已知条件,然后利用基本不等式即可求出cosC 的最小值,可得C的最大值.
解答:在三角形中,由正、余弦定理可将原式转化为:
2ab× =ac•
=ac•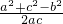 +bc•
+bc•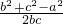 ,化简可得
,化简可得
2c2=a2+b2 ,故 cosC= =
=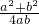 ≥
≥ .
.
故C∈(0°,60°],
故选A.
点评:此题考查学生灵活运用正弦、余弦定理化简求值,会利用基本不等式求函数的最值,属于中档题.
分析:根据正弦、余弦定理化简已知条件,然后利用基本不等式即可求出cosC 的最小值,可得C的最大值.
解答:在三角形中,由正、余弦定理可将原式转化为:
2ab×
 =ac•
=ac•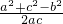 +bc•
+bc•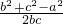 ,化简可得
,化简可得 2c2=a2+b2 ,故 cosC=
 =
=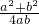 ≥
≥ .
.故C∈(0°,60°],
故选A.
点评:此题考查学生灵活运用正弦、余弦定理化简求值,会利用基本不等式求函数的最值,属于中档题.

练习册系列答案
相关题目
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,