题目内容
设F1、F2分别为椭圆C: =1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2
=1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2 .
.
(1)求椭圆C的焦距;
(2)如果 =2
=2 ,求椭圆C的方程.
,求椭圆C的方程.
【答案】
设焦距为2c,则F1(-c,0),F2(c,0)
∵kl=tan60°=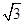
∴l的方程为y=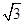 (x-c)
(x-c)
即: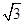 x-y-
x-y-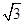 c=0
c=0
∵F1到直线l的距离为2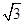
∴c=2
∴椭圆C的焦距为4
(2)设A(x1,y1),B(x2,y2)由题可知y1<0,y2>0
直线l的方程为y=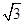 (x-2)
(x-2)
(3a2+b2)y2+4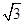 b2y-3b2(a2-4)=0
b2y-3b2(a2-4)=0
∵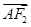 =2
=2 ,∴-y1=2y2,代入①②得
,∴-y1=2y2,代入①②得
得 =
=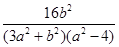 ⑤
⑤
又a2=b2+4 ⑥
由⑤⑥解得a2=9 b2=5
∴椭圆C的方程为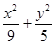 =1
=1
【解析】略

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点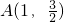 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.