题目内容
已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C的左准线与x轴的交点,过点P的直线l与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线l的斜率的取值范围.
【答案】分析:(I)设出椭圆的方程,根据正方形的面积求出椭圆中参数a的值且判断出参数b,c的关系,根据椭圆的三个参数的关系求出b,c的值得到椭圆的方程.
(II)设出直线的方程,将直线的方程与椭圆方程联立,利用二次方程的韦达定理得到弦中点的坐标,根据中点在正方形的内部,得到中点的坐标满足的不等关系,求出k的范围.
解答:解:(Ⅰ)依题意,设椭圆C的方程为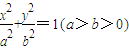 ,焦距为2c,
,焦距为2c,
由题设条件知,a2=8,b=c
所以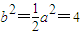
故椭圆的方程为
(II)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0)
显然直线l的斜率存在,所以设直线l的方程为y=k(x+4)
如图,设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x,y)

由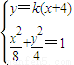 得(1+2k2)x2+16k2x+32k2-8=0.①
得(1+2k2)x2+16k2x+32k2-8=0.①
由△=(16k2)2-4(1+2k2)(32k2-8)>0解得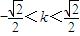 .②
.②
因为x1,x2是方程①的两根,
所以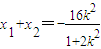 ,于是
,于是
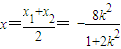 ,
,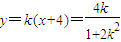 .
.
因为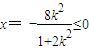 ,所以点G不可能在y轴的右边,
,所以点G不可能在y轴的右边,
又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
所以点G在正方形Q内(包括边界)的充要条件为
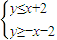 即
即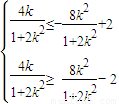 亦即
亦即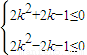
解得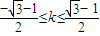 ,此时②
,此时②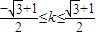 .
.
故直线l斜率的取值范围是
点评:求圆锥曲线的方程时,一般利用待定系数法;解决直线与圆锥曲线的位置关系时,一般采用的方法是将直线方程与圆锥曲线方程联立得到关于某个未知数的二次方程,利用韦达定理来找突破口.
(II)设出直线的方程,将直线的方程与椭圆方程联立,利用二次方程的韦达定理得到弦中点的坐标,根据中点在正方形的内部,得到中点的坐标满足的不等关系,求出k的范围.
解答:解:(Ⅰ)依题意,设椭圆C的方程为
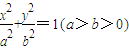 ,焦距为2c,
,焦距为2c,由题设条件知,a2=8,b=c
所以
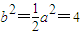
故椭圆的方程为

(II)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0)
显然直线l的斜率存在,所以设直线l的方程为y=k(x+4)
如图,设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x,y)

由
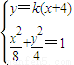 得(1+2k2)x2+16k2x+32k2-8=0.①
得(1+2k2)x2+16k2x+32k2-8=0.①由△=(16k2)2-4(1+2k2)(32k2-8)>0解得
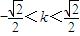 .②
.②因为x1,x2是方程①的两根,
所以
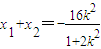 ,于是
,于是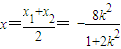 ,
,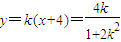 .
.因为
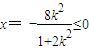 ,所以点G不可能在y轴的右边,
,所以点G不可能在y轴的右边,又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
所以点G在正方形Q内(包括边界)的充要条件为
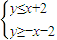 即
即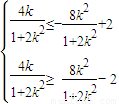 亦即
亦即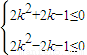
解得
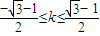 ,此时②
,此时②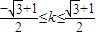 .
.故直线l斜率的取值范围是

点评:求圆锥曲线的方程时,一般利用待定系数法;解决直线与圆锥曲线的位置关系时,一般采用的方法是将直线方程与圆锥曲线方程联立得到关于某个未知数的二次方程,利用韦达定理来找突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 。
。