题目内容
设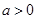 .若曲线
.若曲线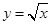 与直线
与直线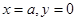 所围成封闭图形的面积为
所围成封闭图形的面积为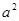 ,则
,则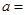 ______.
______.
【答案】
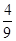
【解析】本试题主要是考查了定积分的几何运用,求解曲边梯形的面积。
根据题意结合定积分的几何意义可知曲线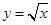 与直线
与直线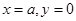 所围成封闭图形的面积为
所围成封闭图形的面积为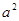 等于
等于
S= ,故解得a的值为
,故解得a的值为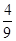 ,故答案为
,故答案为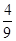 。
。
解决该试题的关键是得到曲线的交点坐标,得到积分上限和下限,然后利用定积分的几何意义表示求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
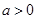 .若曲线
.若曲线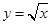 与直线
与直线 所围成封闭图形的面积为
所围成封闭图形的面积为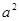 ,则
,则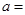 ______.
______.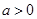 .若曲线
.若曲线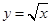 与直线
与直线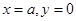 所围成封闭图形的面积为
所围成封闭图形的面积为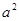 ,则
,则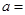 .
.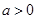 .若曲线
.若曲线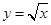 与直线
与直线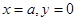 所围成封闭图形的面积为
所围成封闭图形的面积为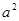 ,则
,则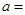 ______.
______.