题目内容
如图,椭圆C: 的右顶点是A,上、下两个顶点分别为B,D,四边形OAMB是矩形(O为坐标原点),点E,P分别是线段OA,AM的中点,
的右顶点是A,上、下两个顶点分别为B,D,四边形OAMB是矩形(O为坐标原点),点E,P分别是线段OA,AM的中点,
(Ⅰ)求证:直线DE与直线BP的交点在椭圆C上;
(Ⅱ)过点B的直线l1,l2与椭圆C分别交于点R,S(不同于B),且它们的斜率k1,k2满足k1k2= ,求证:直线RS过定点,并求出此定点的坐标。
,求证:直线RS过定点,并求出此定点的坐标。
 的右顶点是A,上、下两个顶点分别为B,D,四边形OAMB是矩形(O为坐标原点),点E,P分别是线段OA,AM的中点,
的右顶点是A,上、下两个顶点分别为B,D,四边形OAMB是矩形(O为坐标原点),点E,P分别是线段OA,AM的中点,(Ⅰ)求证:直线DE与直线BP的交点在椭圆C上;
(Ⅱ)过点B的直线l1,l2与椭圆C分别交于点R,S(不同于B),且它们的斜率k1,k2满足k1k2=
 ,求证:直线RS过定点,并求出此定点的坐标。
,求证:直线RS过定点,并求出此定点的坐标。
解:(Ⅰ)由题意,得A(4,0),B(0,2),D(0,-2),E(2,0),P(4,1),
所以直线DE的方程为y=x-2,
直线BP的方程为 ,
,
解方程组 得
得 ,
,
所以直线DE与直线BP的交点坐标为 ,
,
因为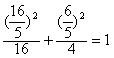 ,
,
所以点 在椭圆
在椭圆 上,
上,
即直线DE与直线BP的交点在椭圆C上。
(Ⅱ)直线BR的方程为y=k1x+2,
解方程组 得
得 ,
,
所以点R的坐标为 ,
,
因为 ,
,
所以直线BS的斜率 ,直线BS的方程为
,直线BS的方程为 ,
,
解方程组 ,
,
所以点S的坐标为 ,
,
所以R,S关于坐标原点O对称,
故R,O,S三点共线,即直线RS过定点O。
所以直线DE的方程为y=x-2,
直线BP的方程为
 ,
,解方程组
 得
得 ,
,所以直线DE与直线BP的交点坐标为
 ,
,因为
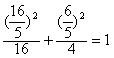 ,
,所以点
 在椭圆
在椭圆 上,
上,即直线DE与直线BP的交点在椭圆C上。
(Ⅱ)直线BR的方程为y=k1x+2,
解方程组
 得
得 ,
,所以点R的坐标为
 ,
,因为
 ,
,所以直线BS的斜率
 ,直线BS的方程为
,直线BS的方程为 ,
,解方程组
 ,
,所以点S的坐标为
 ,
,所以R,S关于坐标原点O对称,
故R,O,S三点共线,即直线RS过定点O。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线
的焦点在x轴上,左、右顶点分别为A1、A,上顶点为B.抛物线C1、C2分别以A、B为焦点,其顶点均为坐标原点O,C1与C2相交于直线 上一点P.
上一点P. ,求
,求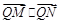 的最小值.
的最小值.
 的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6
的左右顶点为A1,A2,左右焦点为F1,F2,其中F1,F2是A1A2的三等分点,A是椭圆上任意一点,且|AF1|+|AF2|=6 ,若点A在第一象限,求m+n的取值范围;
,若点A在第一象限,求m+n的取值范围;
 的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且
的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且 .
. (O为坐标原点),当
(O为坐标原点),当 时,求实数t的取值范围.
时,求实数t的取值范围.