题目内容
已知正实数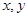 满足
满足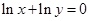 ,且
,且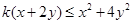 恒成立,则
恒成立,则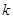 的最大值是________.
的最大值是________.
【答案】
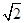
【解析】
试题分析:因为正实数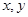 满足
满足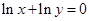 ,
,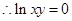 ,即
,即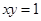 ,可得
,可得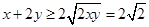 ,
,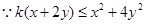 恒成立,即
恒成立,即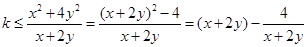 恒成立,即求
恒成立,即求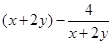 的最小值,令
的最小值,令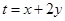 ,则
,则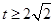 ,令
,令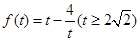 ,则
,则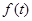 在
在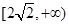 上递增,所以
上递增,所以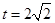 时,
时,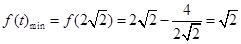 ,
,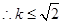 ,则
,则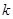 的最大值为
的最大值为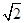 .
.
考点: 1、对数的运算性质,2、基本不等式,3、函数的单调性,4、不等式恒成立问题.

练习册系列答案
相关题目
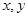 满足
满足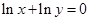 ,且
,且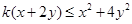 恒成立,则
恒成立,则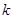 的取值范围是________.
的取值范围是________.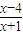 (x≠-1)的反函数是f-1(x).设数列{an}的前n项和为Sn,对任意的正整数都有an=
(x≠-1)的反函数是f-1(x).设数列{an}的前n项和为Sn,对任意的正整数都有an=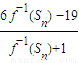 成立,且bn=f-1(an)•
成立,且bn=f-1(an)• ;
;