题目内容
已知二次函数y=f(x)经过点(0,10),导函数![]() =2x-5,当x∈(n,n+1)(n∈N*)时,f(x)是整数的个数,记为an
=2x-5,当x∈(n,n+1)(n∈N*)时,f(x)是整数的个数,记为an![]() 求数列{an}的通项公式.
求数列{an}的通项公式.
答案:
解析:
解析:
解:由![]() =2x-5可设f(x)=x2-5x+c(c为常数).
=2x-5可设f(x)=x2-5x+c(c为常数).
因为f(x)的图象过(0,10),得c=10.
故二次函数为f(x)=x2-5x+10=(x-![]() )2+
)2+![]() .
.
又因x∈(n,n-1)(n∈N*)时,f(x)为整数的个数为an.
f(x)在(1,2)上的值域为[4,6],∴a1=2.
f(x)在(2,3)上的值域为[![]() ,4],∴a2=1.
,4],∴a2=1.
当n≥3时,f(x)在![]() 上单调递增,其值域为
上单调递增,其值域为![]()
∴an=f(n+1)-f(n)=2n-4.
∴an=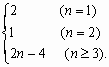

练习册系列答案
相关题目

 =6x-2,数列{
=6x-2,数列{ }的前n项和为
}的前n项和为 ,点(n,
,点(n, ,
, 是数列{
是数列{ }的前n项和,求使得
}的前n项和,求使得