题目内容
已知向量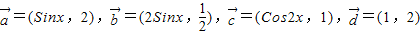 ,又二次函数f(x)的图象开口向上,其对称轴为x=1.
,又二次函数f(x)的图象开口向上,其对称轴为x=1.(1)分别求
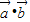 和
和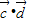 的取值范围
的取值范围(2)当x∈[0,π]时,求不等式
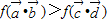 的解集.
的解集.
【答案】分析:(1)利用向量的数量积公式求出 ,再利用三角函数的有界性求出数量积的范围.
,再利用三角函数的有界性求出数量积的范围.
(2)利用二次函数的单调性去掉抽象函数的对应法则,再利用二倍角的余弦公式及三角函数的图象求出x的范围
解答:解:(1)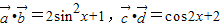
又0≤Sin2x≤1,-1≤Cos2x≤1,
∴ .
.
(2)∵x∈[0,π],
∴0≤Sin2x≤1,-1≤Cos2x≤1,
∴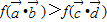 ?f(2sin2x+1)>f(cos2x+2)
?f(2sin2x+1)>f(cos2x+2)
又依题意f(x)在[1,+∞)上是增函数.
由(1)知,2Sin2x+1>Cos2x+2,即4Sin2x>2,
∴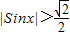 ,又x∈[0,π],
,又x∈[0,π],
∴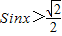 ,
,
∴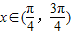 .
.
点评:本题考查向量的数量积公式、三角函数的有界性、二次函数的单调性、及二倍角的余弦公式.
 ,再利用三角函数的有界性求出数量积的范围.
,再利用三角函数的有界性求出数量积的范围.(2)利用二次函数的单调性去掉抽象函数的对应法则,再利用二倍角的余弦公式及三角函数的图象求出x的范围
解答:解:(1)
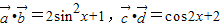
又0≤Sin2x≤1,-1≤Cos2x≤1,
∴
 .
.(2)∵x∈[0,π],
∴0≤Sin2x≤1,-1≤Cos2x≤1,
∴
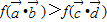 ?f(2sin2x+1)>f(cos2x+2)
?f(2sin2x+1)>f(cos2x+2)又依题意f(x)在[1,+∞)上是增函数.
由(1)知,2Sin2x+1>Cos2x+2,即4Sin2x>2,
∴
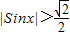 ,又x∈[0,π],
,又x∈[0,π],∴
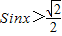 ,
,∴
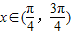 .
.点评:本题考查向量的数量积公式、三角函数的有界性、二次函数的单调性、及二倍角的余弦公式.

练习册系列答案
相关题目