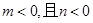题目内容
一次函数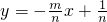 的图象同时经过第一、三、四象限的必要但不充分条件是
的图象同时经过第一、三、四象限的必要但不充分条件是
- A.m>1,且n<1
- B.mn<0
- C.m>0,且n<0
- D.m<0,且n<0
B
分析:由一次函数的图象和性质,我们可以求出一次函数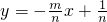 的图象同时经过第一、三、四象限的等价命题,进而逐一分析已知中四个答案中的条件与一次函数
的图象同时经过第一、三、四象限的等价命题,进而逐一分析已知中四个答案中的条件与一次函数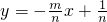 的图象同时经过第一、三、四象限的充要关系,即可得到答案.
的图象同时经过第一、三、四象限的充要关系,即可得到答案.
解答:若一次函数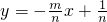 的图象同时经过第一、三、四象限
的图象同时经过第一、三、四象限
则 >0,
>0, <0,即m>0且n<0
<0,即m>0且n<0
故“m>1,且n<1”是“一次函数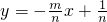 的图象同时经过第一、三、四象限的”的不充分也不必要条件;
的图象同时经过第一、三、四象限的”的不充分也不必要条件;
“mn<0”是“一次函数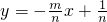 的图象同时经过第一、三、四象限的”的必要但不充分条件;
的图象同时经过第一、三、四象限的”的必要但不充分条件;
“m>0,且n<0”是“一次函数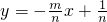 的图象同时经过第一、三、四象限的”的充要条件;
的图象同时经过第一、三、四象限的”的充要条件;
“m<0,且n<0”是“一次函数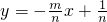 的图象同时经过第一、三、四象限的”的不充分也不必要条件;
的图象同时经过第一、三、四象限的”的不充分也不必要条件;
故选B
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,其中根据一次函数的图象和性质,将已知中条件等价转化为m>0且n<0,是解答本题的关键.
分析:由一次函数的图象和性质,我们可以求出一次函数
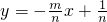 的图象同时经过第一、三、四象限的等价命题,进而逐一分析已知中四个答案中的条件与一次函数
的图象同时经过第一、三、四象限的等价命题,进而逐一分析已知中四个答案中的条件与一次函数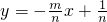 的图象同时经过第一、三、四象限的充要关系,即可得到答案.
的图象同时经过第一、三、四象限的充要关系,即可得到答案.解答:若一次函数
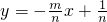 的图象同时经过第一、三、四象限
的图象同时经过第一、三、四象限则
 >0,
>0, <0,即m>0且n<0
<0,即m>0且n<0故“m>1,且n<1”是“一次函数
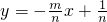 的图象同时经过第一、三、四象限的”的不充分也不必要条件;
的图象同时经过第一、三、四象限的”的不充分也不必要条件;“mn<0”是“一次函数
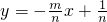 的图象同时经过第一、三、四象限的”的必要但不充分条件;
的图象同时经过第一、三、四象限的”的必要但不充分条件;“m>0,且n<0”是“一次函数
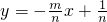 的图象同时经过第一、三、四象限的”的充要条件;
的图象同时经过第一、三、四象限的”的充要条件;“m<0,且n<0”是“一次函数
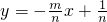 的图象同时经过第一、三、四象限的”的不充分也不必要条件;
的图象同时经过第一、三、四象限的”的不充分也不必要条件;故选B
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,其中根据一次函数的图象和性质,将已知中条件等价转化为m>0且n<0,是解答本题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
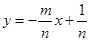 的图象同时经过第一、三、四象限的一个充分不必要条件是 。
的图象同时经过第一、三、四象限的一个充分不必要条件是 。 的图象同时经过第一、三、四象限的必要不充分条件是( )
的图象同时经过第一、三、四象限的必要不充分条件是( ) B.
B.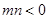
 D.
D.
 的图象同时经过第一、三、四象限的必要但不充分条件是( )
的图象同时经过第一、三、四象限的必要但不充分条件是( )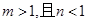 B.
B.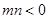
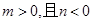 D.
D.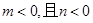
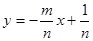 的图象同时经过第一、三、四象限的必要但不充分条件是( )
的图象同时经过第一、三、四象限的必要但不充分条件是( )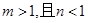 B.
B.
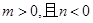 D.
D.