题目内容
已知函数f(x)=|x+2|+x-2
(1)用分段函数的形式表示f(x),
(2)画出函数的图象,并写出函数的单调区间、值域.
(1)用分段函数的形式表示f(x),
(2)画出函数的图象,并写出函数的单调区间、值域.
分析:(1)根据绝对值的意义,结合分类讨论去掉函数式中的绝对值,即可化简出分段函数的形式表示f(x)的式子;
(2)根据函数式的在不同两段的解析式,结合一次函数图象的作法,即可作出函数如图所示的图象,再根据图象不难写出函数的单调区间与值域.
(2)根据函数式的在不同两段的解析式,结合一次函数图象的作法,即可作出函数如图所示的图象,再根据图象不难写出函数的单调区间与值域.
解答:解:(1)∵当x≥-2时,|x+2|=x+2,f(x)=x+2+x-2=2x;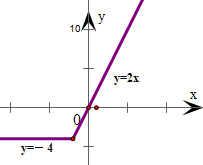
当x<-2时,|x+2|=-x-2,f(x)=-x-2+x-2=-4
因此,用分段函数的形式表示函数,可得f(x)=
;
(2)画出函数的图象,如右图所示--------(8分),
根据图象,可得
函数的单调增区间为[-2,+∞)--------(12分)
值域为[-4,+∞)------(16分).
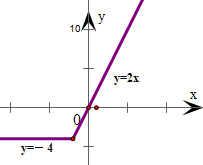
当x<-2时,|x+2|=-x-2,f(x)=-x-2+x-2=-4
因此,用分段函数的形式表示函数,可得f(x)=
|
(2)画出函数的图象,如右图所示--------(8分),
根据图象,可得
函数的单调增区间为[-2,+∞)--------(12分)
值域为[-4,+∞)------(16分).
点评:本题给出带绝对值的函数,求函数的分段形式的表达式并求单调区间与值域.着重考查了绝对值的意义、函数图象的作法和函数的单调性等知识,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|