题目内容

将函数y=sin(x+
π
6
)的图象向左平移
π
4
个单位长度，再将图象上各点的横坐标变为原来的2倍（保持各点坐标不变），则所得到图象的解析式为
 
．
分析：先根据左加右减的原则左右平移，然后根据横坐标的变化进行左右伸缩变换．
解答：解：将函数y=sin(x+
π
6
)的图象向左平移
π
4
个单位长度得y=sin（x+
5π
12
），
再将图象上各点的横坐标变为原来的2倍（保持各点坐标不变）得y=sin(
x
2
+
5
12
π)
故答案为：y=sin(
x
2
+
5
12
π)
点评：本题主要考查三角函数的平移变换．属基础题．
练习册系列答案
相关题目
将函数y=sin(x+
π
6
)的图象按向量
a
=(-m，0)平移所得的图象关于y轴对称，则m最小正值是（　　）
A、
π
3
B、
π
6
C、
2π
3
D、
5π
6
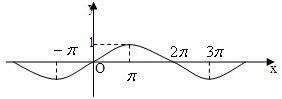精英家教网已知函数y=sinωx（ω＞0）在一个周期内的图象如图所示，要得到函数y=sin（
1
2
x+
π
12
）的图象，则需将函数y=sinωx的图象（　　）
A、向右平移
π
12
B、向左平移
π
12
C、向右平移
π
6
D、向左平移
π
6
将函数y=sin(x+
π
4
)的图象上各点的横坐标伸长到原来2的倍，再向左平移
π
2
个单位，所得图象的函数解析式是（　　）
将函数y=sin(x+
π
3
)的图象向右平移
π
6
个单位，再向上平移2个单位所得图象对应的函数解析式是（　　）
若将函数y=sinωx的图象向右平移
π
3
个单位长度后，与函数y=sin(ωx+
π
4
)的图象重合，则ω的一个值为（　　）
A、
3
4
B、
4
3
C、-
3
4
D、-
4
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网