题目内容
(1)已知函数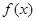 的定义域为
的定义域为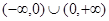 ,
,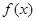 是奇函数,且当
是奇函数,且当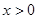 时,
时,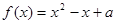 ,若函数
,若函数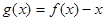 的零点恰有两个,则实数
的零点恰有两个,则实数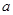 的取值范围是( )
的取值范围是( )
(2)对于函数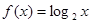 在其定义域内任意的
在其定义域内任意的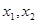 且
且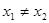 ,有如下结论:
,有如下结论:
①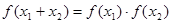 ;
;
②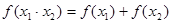 ;
;
③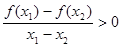 ;
;
④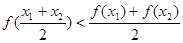 .
.
上述结论中正确结论的序号是________.
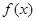 的定义域为
的定义域为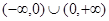 ,
,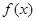 是奇函数,且当
是奇函数,且当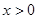 时,
时,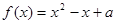 ,若函数
,若函数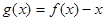 的零点恰有两个,则实数
的零点恰有两个,则实数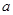 的取值范围是( )
的取值范围是( )A.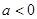 | B.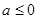 |
C.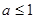 | D.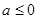 或 或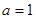 |
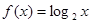 在其定义域内任意的
在其定义域内任意的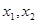 且
且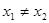 ,有如下结论:
,有如下结论:①
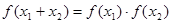 ;
;②
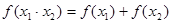 ;
;③
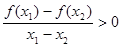 ;
;④
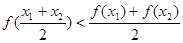 .
.上述结论中正确结论的序号是________.
(1)D;(2)②③
试题分析:(1)要使函数
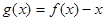 的零点恰有两个,则根据函数是奇函数,则只需要当
的零点恰有两个,则根据函数是奇函数,则只需要当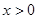 时,函数
时,函数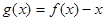 的零点恰有一个即可.
的零点恰有一个即可.(2)利用对数的基本运算性质进行检验即可.
(1)因为
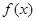 是奇函数,所以
是奇函数,所以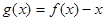 也是奇函数,所以要使函数
也是奇函数,所以要使函数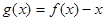 的零点恰有两个,则只需要当
的零点恰有两个,则只需要当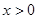 时,函数
时,函数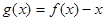 的零点恰有一个即可.
的零点恰有一个即可.由
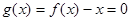 得,
得,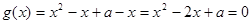 ,
,若
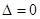 ,即
,即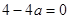 ,解得
,解得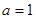 .
.若
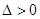 ,要使当
,要使当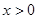 时,函数
时,函数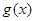 只有一个零点,则
只有一个零点,则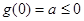 ,
,所以此时
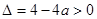 ,
,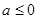 ,解得
,解得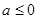 .
.综上
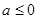 或
或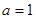 .
.故选D.
(2)利用对数的基本运算性质进行检验:
①
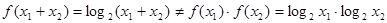 ;
;②
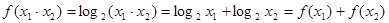 ;
;③
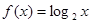 在
在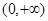 单调递增,可得
单调递增,可得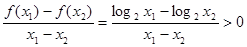 ;
;④
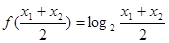 ,
,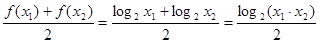 ,由基本不等式可得
,由基本不等式可得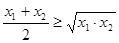 ,从而可得
,从而可得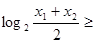
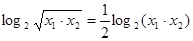 .
.故答案为:②③.

练习册系列答案
相关题目
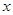 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与
(亿千瓦时)与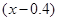 元成反比例.又当
元成反比例.又当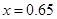 时,
时,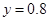 .
.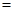 用电量
用电量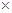 (实际电价-成本价)]
(实际电价-成本价)] (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式 ,
, 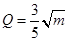 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资 (单位:万元)
(单位:万元) (单位:万元)关于
(单位:万元)关于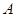 处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的
处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的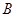 处,乙厂到河岸的垂足
处,乙厂到河岸的垂足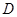 与
与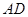 之间合建一个供水站
之间合建一个供水站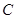 ,从供水站到甲厂和乙厂的水管费用分别为每千米3
,从供水站到甲厂和乙厂的水管费用分别为每千米3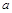 元和5
元和5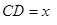 千米,设总的水管费用为
千米,设总的水管费用为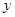 元,如图所示,
元,如图所示,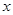 的函数表达式;
的函数表达式;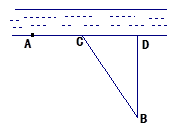
 .
.
 表示
表示 的面积;
的面积;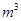 ,深为2
,深为2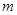 的无盖水池,如果池底与池壁的造价每平方米分别是120元和80元,则水池的最低造价为 元.
的无盖水池,如果池底与池壁的造价每平方米分别是120元和80元,则水池的最低造价为 元.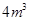 ,高为1m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是( )
,高为1m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是( )
 ,
, 的整数部分用
的整数部分用 表示,则
表示,则 的值是 .
的值是 .